Question

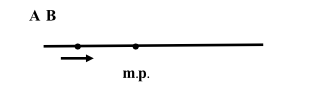
A particle is an oscillating simple harmonically with angular frequency and amplitude. It is at a point (A) at a certain instant (shown in the figure). At this instant, it is moving towards the mean position (B). It takes time to reach the mean position (B). If the time period of oscillation is , the average speed between A and B is:

(a)$\dfrac{A\sin \omega t}{t}$
(b)$\dfrac{A\cos \omega t}{t}$
(c)$\dfrac{A\sin \omega t}{T}$
(d)$\dfrac{A\cos \omega t}{T}$

Answer 1

Hint:In order to calculate the average speed between A and B, we need to use the formula of S.H.M,
Step by step solution, Velocity $(v)=\dfrac{\int dx}{\int dt}$.

Step by step solution,
Let the S.H.M be$x=A\sin \omega t$
$dx=A\omega \cos \omega t\text{ }\!\!~\!\!\text{ }dt$
Velocity$(v)=\dfrac{\int dx}{\int dt}$
So, mean speed between A to B is,
$=\dfrac{\mathop{\int }_{0}^{t}A\omega \cos \omega t dt}{\mathop{\int }_{0}^{t}dt}$
$=\dfrac{A\omega \dfrac{\sin \omega t}{\omega }}{t}$
$=\dfrac{A\sin \omega t}{t}$

Thus, the correct answer to this question is option (a).

Additional Information:Simple harmonic motion is the motion in which the object moves to and fro along a line.The law of conservation of energy states that energy can neither be created nor destroyed. Therefore, the total energy in simple harmonic motion will always be constant. However, kinetic energy and potential energy are interchangeable. Given below is the graph of kinetic and potential energy vs instantaneous displacement.In the simple harmonic motion, the displacement of the object is always in the opposite direction of the restoring force.And, the simple harmonic motion is always oscillatory.Simple harmonic motion examples: the motion of a pendulum, motion of a spring, etc.

Note:While solving this question, one should be familiar with the concept of S.H.M. Some concepts are provided above for the reference.