Question

A particle executing SHM of amplitude 4 cm and T = 4 seconds. The time taken by it to move from positive extreme position to half of the amplitude is:
A. 1 s
B. \[\dfrac{1}{3}\] s
C. \[\dfrac{2}{3}\] s
D. \[\sqrt{\dfrac{3}{2}}\] s

Answer 1

Hint: In this question we have been asked to calculate the time taken by a particle in SHM to move from its positive extreme position to half of the amplitude. It is given that the amplitude of the SHM is 4 cm and the time period is 4 seconds. Therefore, to solve this question, we shall use the equation of SHM. This equation deals with the amplitude, time period, and angular velocity of SHM.

Formula used:- \[y=A\cos \omega t\]

Complete step by step solution:
 In the question, it is given that the amplitude of SHM is 4 cm and T = 4 seconds.
Consider the diagram given below.

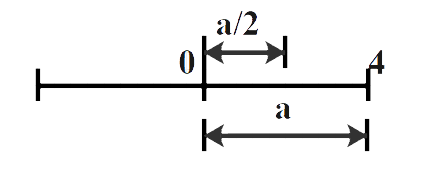
We can say that the distance from the extreme positive position is half the amplitude.
To calculate the time required to move this distance
We know that,
\[y=A\cos \omega t\]
Substituting the values
We get,
\[\dfrac{A}{2}=A\cos \omega t\]
On solving we get,
\[\cos \omega t=\dfrac{1}{2}\] ………. (1)
But we know that,
\[\cos \dfrac{\pi }{3}=\dfrac{1}{2}\] ………… (2)
From (1) and (2)
We get,
\[\omega t=\dfrac{\pi }{3}\] …………. (3)
We also know that,
\[\omega =\dfrac{2\pi }{T}\] ………….. (4)
Now, from (3) and (4)
We get,
\[\dfrac{2\pi }{T}t=\dfrac{\pi }{3}\]
It is given that T = 4 seconds
Therefore,
\[t=\dfrac{2}{3}s\]
Therefore, the correct answer is option C.

Note: The motion in which the restoring force is directly proportional to the displacement of the body from its mean position is known as SHM or Simple Harmonic Motion. The restoring force in SHM always acts towards the equilibrium position. In SHM the maximum displacement on either side of the equilibrium position is equal for both sides.