Question

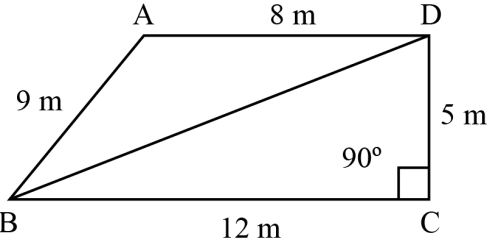
A park, in the shape of a quadrilateral ABCD, has \[\angle C = 90^\circ \], \[AB = 9{\rm{ m}}\], \[{\rm{ }}BC = 12{\rm{ m}}\] $CD = 5\;{\rm{m}}$ and \[AD = 8{\rm{ m}}\]. How much area does it occupy?

Answer 1

Hint: To find the total area of park divide the quadrilateral to two triangles that is $\Delta ABD$ and $\Delta BCD$. The total area of park will be= area ΔABD + area ΔBCD.

Complete step by step solution:
The angle of C is $90^\circ $.
The length of AB is $9\;{\rm{m}}$.
The length of BC is $12\;{\rm{m}}$.
The length of the CD is $5\;{\rm{m}}$.
The length of AD is $8\;{\rm{m}}$.
The\[\Delta BCD\]is a right angled triangle since$\angle C = 90^\circ $.
The formula for right-angled triangle is,
\[\begin{array}{c}
{\rm{Area of }}\Delta BCD{\rm{ }} = \dfrac{1}{2} \times BC \times CD\\
 = \dfrac{1}{2} \times 12 \times 5\;{{\rm{m}}^2}\\
 = 30\;{{\rm{m}}^2}
\end{array}\]
The general formula for area of triangle is,
${\rm{A}} = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $…..(1)
Here, $s$is the semi-perimeter and $a,\;b,\;c$are the sides of the triangle.
To find the value of BD we apply Pythagora's theorem since $\angle C = 90^\circ $.
$\begin{array}{c}
B{D^2} = B{C^2} + C{D^2}\\
 = {\left( {12} \right)^2} + {\left( 5 \right)^2}\\
 = 144 + 25\\
 = 169
\end{array}$
Hence, taking square root on both sides we obtain,
$\begin{array}{c}
BD = \sqrt {169} \\
 = \sqrt {{{13}^2}} \\
 = 13\,\;{\rm{m}}
\end{array}$
The formula for semi-perimeter is,
$s = \dfrac{{a + b + c}}{2}$
Substitute $a,\;b,\;c$values in$s$,
$\begin{array}{c}
s = \dfrac{{AD + AB + BD}}{2}\\
 = \dfrac{{8 + 9 + 13}}{2}\\
 = \dfrac{{30}}{2}\\
 = 15\;{\rm{m}}
\end{array}$

On putting, the value of s in the equation (1).
$\begin{array}{c}
{\rm{Area of }}\Delta {\rm{ABD }} = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} \\
 = \sqrt {15\left( {15 - 8} \right)\left( {15 - 9} \right)\left( {15 - 13} \right)} \\
 = \sqrt {15\left( 7 \right)\left( 6 \right)\left( 2 \right)} {\rm{ }}{{\rm{m}}^2}\\
 = 35.46{\rm{ }}{{\rm{m}}^2}
\end{array}$
Hence, the area of the triangle \[\Delta ABD{\rm{ }} = {\rm{ }}35.46{\rm{ }}{{\rm{m}}^2}.\]
\[\begin{array}{c}
{\rm{The area of park }} = {\rm{ Area of }}\Delta {\rm{ABD }} + {\rm{Area of }}\Delta {\rm{BCD}}\;\\
 = 35.46{\rm{ }} + {\rm{ }}30{\rm{ }}{{\rm{m}}^2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\
 = 65.46{\rm{ }}{{\rm{m}}^2}\;
\end{array}\]

Therefore, the area of park is \[65.46{\rm{ }}{{\rm{m}}^2}\;\].

Note: If $\angle C = 90^\circ $, so we will use right angle triangle formula if $\angle C$ is not equal to $90^\circ $ then, right angle triangle formula should not be used instead of which we need to use triangle formula.