Question

A park has a radius of 10m. If a vehicle goes round it at average speed of 18 km/hr, what should be the proper angle of banking $\left[ {g = 10m{s^{ - 2}}} \right]$
A. ${\tan ^{ - 1}}\left( {\dfrac{1}{4}} \right)$
B. ${\tan ^{ - 1}}\left( {\dfrac{3}{2}} \right)$
C. ${\tan ^{ - 1}}\left( {\dfrac{1}{2}} \right)$
D. ${\tan ^{ - 1}}\left( {\dfrac{2}{3}} \right)$

Answer 1

Hint: To solve the question, it is necessary to understand the definition of banking. Banking of roads is the phenomenon in which the edges are raised for curved roads above the inner edge to provide the necessary centripetal force to the vehicles so that they take a safe turn.

Complete step by step answer:
We have seen the definition of the term banking of roads. But we need to understand the necessity of banking the roads.
When the vehicle is moving on a flat curved road, there is a centripetal force acting on the vehicle when it is moving in the circular path. But still, the car moves in the circular path without deviating. However, if the velocity crosses beyond a limit, the centripetal force overpowers and the car deviates from the circular path and moves towards the center.
The best way to avoid this incident is by decreasing the vehicle speed around the corner.
However, it is not always practical to decrease the speed around the corners in cases like highways where the cars will be at a very high speed. Hence, it is advisable to increase the speed limit without altering the curvature of the road.
This can be done by the process of banking wherein the outer edge is raised above the inner edge by an angle called the angle of banking.

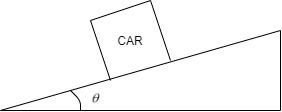
Here, $\theta $ is called the angle of banking, through which the outer edge of the road is raised.
The minimum velocity required to be maintained without the banking is –
$v^2 = rg$
where r = radius of curvature, g = acceleration due to gravity.
Now, if the banking is provided, we get
$v^2 = rg\tan \theta $
where $\theta $ is called the angle of banking.
Given, velocity, $v = 18kmph = 18 \times \dfrac{5}{{18}} = 5m{s^{ - 1}}$
Radius of the turn, $r = 10m$
Acceleration due to gravity, $g = 10m{s^{ - 2}}$
Substituting the values, we get
$\Rightarrow v^2 = rg\tan \theta $
$\Rightarrow {5^2} = 10 \times 10 \times \tan \theta $
$\Rightarrow \tan \theta = \dfrac{{25}}{{100}} = \dfrac{1}{4} $
$\therefore \theta = {\tan ^{ - 1}}\left( {\dfrac{1}{4}} \right) $

Therefore, the correct option is Option A.

Note:
Now, let us see the case if there was no banking in the road. Then, the minimum velocity to be maintained will be equal to :
$v^2 = rg = 10 \times 10 = 100 $
$\Rightarrow v = 10m{s^{ - 1}} = \dfrac{{18}}{5} \times 10 = 18 \times 2 = 36kmph $
Here, we can see that without the banking, the vehicle would have to maintain a higher speed of limit to avoid the overturning.