Question

A parallelepiped is formed by planes drawn through the points $P(6,8,10)$ and $Q(3,4,8)$ parallel to the coordinate planes. Find the length of edges and diagonals of the parallelepiped.

Answer 1

Hint: For solving this question first we will draw planes through the points $P(6,8,10)$ and $Q(3,4,8)$ parallel to the coordinate planes. After that, we will prove that parallelepiped formed by the given planes will be a cuboid and we will find its dimensions. Moreover, we will use the formula $\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}$ to find the body diagonal of the cuboid of length $l$ , breadth $b$ and height $h$ .

Complete step by step solution:
Given:
We have to find the length of edges and diagonals of the parallelepiped formed by planes drawn through the points $P(6,8,10)$ and $Q(3,4,8)$ parallel to the coordinate planes.
Now, before we proceed we should know that if there is a point $A\left( {{x}_{1}},{{y}_{2}},{{z}_{2}} \right)$ then $x={{x}_{1}}$ , $y={{y}_{1}}$ and $z={{z}_{1}}$ planes will pass through point $A\left( {{x}_{1}},{{y}_{2}},{{z}_{2}} \right)$ and parallel to the coordinate planes.
Now, from the above discussion, we conclude that, $x=6$ , $y=8$ and $z=10$ planes will be passing through point $P(6,8,10)$ and parallel to the coordinate planes. For more clarity look at the figure given below:

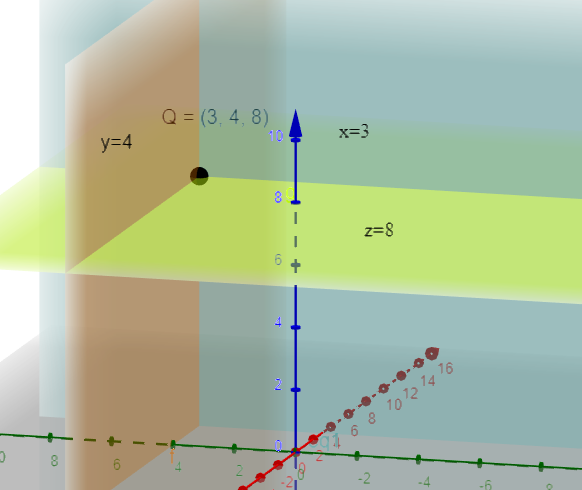
Now, from the above discussion, we conclude that, $x=3$ , $y=4$ and $z=8$ planes will be passing through point $Q(3,4,8)$ and parallel to the coordinate planes. For more clarity look at the figure given below:

Now, there are the following six planes:
$\begin{align}
  & x=6\text{ and }x=3 \\
 & y=8\text{ and y}=4 \\
 & z=10\text{ and }z=8 \\
\end{align}$
Now, parallelepiped formed by the above six planes will be a cuboid. For more clarity look at the figure given below:

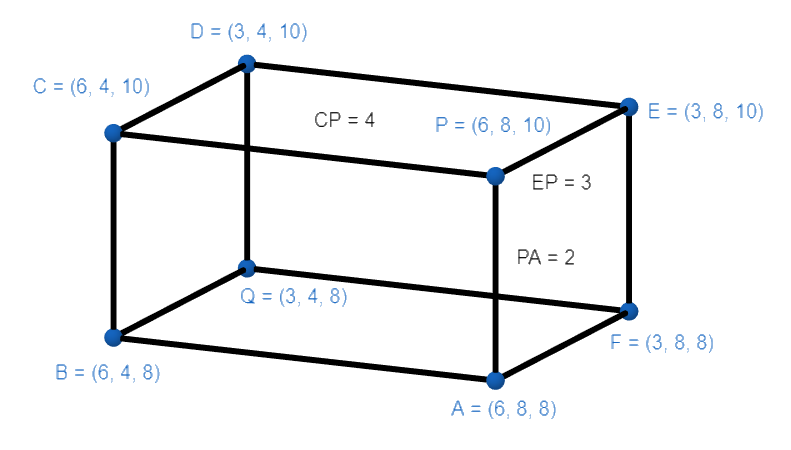
Now, to find the dimensions of the cuboid we will find the distance between the following planes:
$\begin{align}
  & x=6\text{ and }x=3 \\
 & y=8\text{ and y}=4 \\
 & z=10\text{ and }z=8 \\
\end{align}$
Now, as the above three pairs of planes are parallel so, we will simply find the difference in their values.
For length find the distance between planes $y=8$ and $y=4$ , for breadth find the distance between planes $x=6$ and $x=3$ , and for height find the distance between planes $z=10$ and $z=8$ Then,
$\begin{align}
  & Length=l=8-4=4 \\
 & Breadth=b=6-3=3 \\
 & Height=h=10-8=2 \\
\end{align}$
Now, from the above result, we conclude that the length, breadth and height of the cuboid will be 4, 3 and 2 units respectively.
Now, as we know that length of the body diagonal of the cuboid of length $l$ , breadth $b$ and height $h$ is $\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}$ . Then,
Length of the body diagonal $=\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}=\sqrt{{{4}^{2}}+{{3}^{2}}+{{2}^{2}}}=\sqrt{16+9+4}=\sqrt{29}$ units.
Now, we conclude that the required parallelepiped will be a cuboid of length, breadth and height of the cuboid will be 4, 3 and 2 units respectively and length of the diagonal of the parallelepiped will be $\sqrt{29}\approx 5.385$ units.

Note: The coordinates of the vertices of the parallelepiped can be found out by finding the point of intersection of the planes taken 3 at a time. For example, the point of intersection of the planes x=6, y=8 and z=10 is (6,8,10), which is the coordinate of the vertex P.