Question

A parallel sides slab ABCD of refractive index $2$ is sandwiched between two slabs of refractive indices $\sqrt{2}$ and $\sqrt{3}$ as shown in the figure. The minimum value of the angle such that the ray PQ suffers total internal reflection at both the surfaces AB and CD

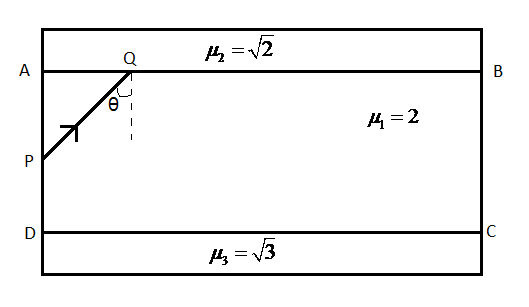
$A)\text{ }{{30}^{0}}$ $B)\text{ 4}{{\text{5}}^{0}}$ $C)\text{ }{{60}^{0}}$ $D)\text{ }{{75}^{0}}$

Answer 1

Hint: This problem can be solved by realizing the fact that for suffering total internal reflection at both surfaces, the angle of incidence at both surfaces must be greater than or equal to the critical angle for the two media. Hence, by using the formula for the critical angle in terms of the refractive indices of the two media, we can get the required angle.

Formula used:
${{\theta }_{C}}={{\sin }^{-1}}\left( \dfrac{{{n}_{2}}}{{{n}_{1}}} \right)$

Complete step-by-step answer:
We will find out the critical angle for total internal reflection at both surfaces. So, let us write the formula for the critical angle.
For a light ray that undergoes total internal reflection while going from a medium of refractive index ${{n}_{1}}$ to a medium of refractive index ${{n}_{2}}$ and gets internally reflected at the surface, the critical angle ${{\theta }_{C}}$ is given by
${{\theta }_{C}}={{\sin }^{-1}}\left( \dfrac{{{n}_{2}}}{{{n}_{1}}} \right)$ $\left( {{n}_{2}}<{{n}_{1}} \right)$ --(1)
Now, let us analyze the question.

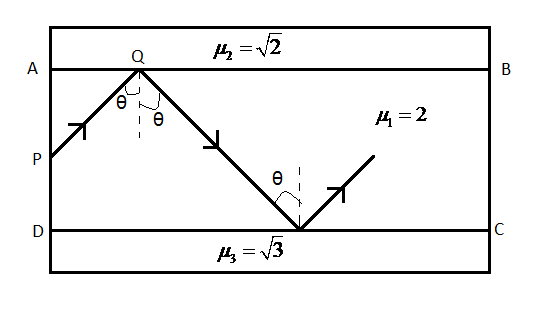
Here, the required situation, that is, the ray of light reflecting at both interfaces is shown. By geometry, the angles of incidence at both interfaces will be $\theta $ as by the laws of reflection, the angle of reflection at the first interface is equal to the angle of incidence.
Now, using (1), for the first interface at AB, the critical angle ${{\theta }_{C1}}$ will be equal to
${{\theta }_{C1}}={{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right)={{\sin }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right)={{45}^{0}}$ $\left( \because {{\sin }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right)={{45}^{0}} \right)$
Now, for suffering total internal reflection, the angle of incidence must be greater than or equal to this critical angle.
$\therefore \theta \ge {{\theta }_{C1}}$ $\therefore \theta \ge {{45}^{0}}$ --(2)
Now, Now, using (1), for the second interface at CD, the critical angle ${{\theta }_{C2}}$ will be equal to
${{\theta }_{C2}}={{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)={{60}^{0}}$ $\left( \because {{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)={{60}^{0}} \right)$
Now, for suffering total internal reflection, the angle of incidence must be greater than or equal to this critical angle.
$\therefore \theta \ge {{\theta }_{C2}}$ $\therefore \theta \ge {{60}^{0}}$ --(3)
Now, from (2) and (3), we can see that
$\theta \ge {{45}^{0}}$ and $\theta \ge {{60}^{0}}$ Therefore, obviously $\theta \ge {{60}^{0}}$.
Now, since we require the minimum value of the angle $\theta $,
$\therefore \theta ={{60}^{0}}$
Hence, we have got the required minimum value of the angle $\theta $ as ${{60}^{0}}$.
Therefore, the correct option is $C)\text{ }{{60}^{0}}$.

So, the correct answer is “Option C”.

Note: Students must note that it is not necessary that for suffering total internal reflection at an interface, the light ray should have an angle of incidence exactly equal to the critical angle. In fact, the critical angle is only the minimum amount of angle of incidence at which the light ray suffers total internal reflection and therefore, for all angles greater than this value of the critical angle, the light ray will undergo total internal reflection at the interface.