Question

A parachutist of weight w strikes the ground with his legs fixed and comes to rest with an upward acceleration of magnitude $3$g. The force exerted on him by the ground during landing is?

Answer 1

Hint: Normal force is the force which comes into action when two bodies come into contact. Direction of normal force is opposite to the applied force on the contact. Also we will keep in mind the direction of gravitational force and sign convention of all these forces.

Complete step by step answer:
As the parachutist strike the ground the force it exerts on the ground by the virtue of its
Weight (mass times g(gravitational acceleration)) and the ground exerts an normal force on the parachutist which we call the normal force , the normal force is the reason for the
Upward acceleration of $3g$ .Let the mass of the parachutist be m than w(weight = force exerted on the earth due to gravity) than $w = mg$.

Drawing the free body diagram for the given situation we get

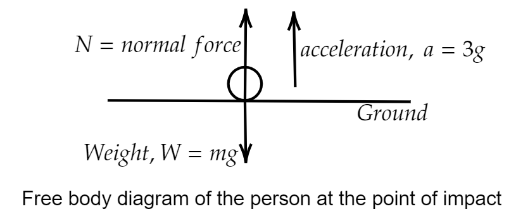
Where, \[w = mg\], $N$ = normal force (force exerted on the parachutist by the ground),$F$ = force with which parachutist moves upwards = m(mass of the parachutist) \[ \times \] \[3g\] (upward acceleration of the parachutist).
The force equation will be taking upward direction to be positive and downward direction to be negative we get,
\[N - mg = m(3g)\]
\[ \Rightarrow N = 3mg + mg\]
\[ \therefore N = 4mg\]

So we can say the force exerted on the parachutist by ground is equal to $4$ times the weight of the parachutist.

Note:Remember that when by Newton’s law we write the equation of motion of a body, we only calculate the net force acting on the body, we do not need to consider the forces exerted by the body as it has no effect on the body. Normal force is a contact force by the virtue of which objects cannot move through each other. So, normal force only exists when the person comes in contact with the surface. Before the point of impact there is no normal force acting on the body. So, before the point of impact the equation of motion of the body is, \[{F_{air}} - mg = ma\] where, \[{F_{air}}\] is the upward air thrust.