Question

A parachute of mass m starts coming down with a constant acceleration a. Determine the ballast mass to be released from the parachute to have an upward acceleration of the same magnitude. Neglect air drag.

A. $\dfrac{{2ma}}{{a + g}}$
B. $\dfrac{{ma}}{{a - g}}$
C. $\dfrac{{ma}}{{a + g}}$
D. $\dfrac{{2ma}}{{a - g}}$

Answer 1

Hint: As the parachute is moving downwards initially, the force exerted by it will be gravitational force minus upward thrust. Then a ballast mass is dropped and the parachute now moves upwards with an upward acceleration, here the new mass will be initial mass minus ballast mass and the force exerted by the parachute will be the upward thrust minus gravitational force. Use this info to solve the given problem.

Complete step by step answer:We are given a parachute of mass m that starts coming down with a constant acceleration a.
We have to determine the ballast mass to be released from the parachute to have an upward acceleration of the same magnitude.
Initially the acceleration is downwards and the parachute moves downwards. Let the upward thrust be T.

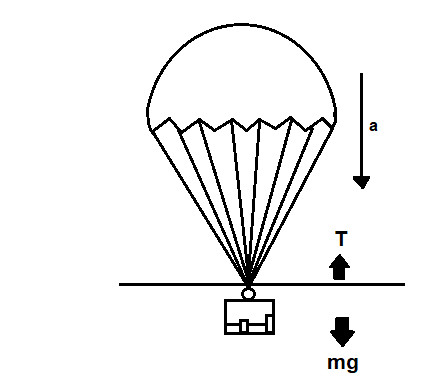
Force is the product of mass of the body and acceleration of it.
Therefore, Force exerted by parachute before dropping the mass is
$ma = mg - T \Rightarrow eq\left( 1 \right)$
Let the ballast mass which is to be released is ${m^1}$
Now the final mass of the parachute will be $m - {m^1}$
After dropping the mass, the acceleration now is upwards and the parachute moves upwards.

Therefore, Force exerted by parachute after dropping the mass is
$
  \left( {m - {m^1}} \right)a = T - \left( {m - {m^1}} \right)g \\
   \Rightarrow ma - {m^1}a = T - mg + {m^1}g \Rightarrow eq\left( 2 \right) \\
 $
On adding equation 1 with equation 2, we get
$
  ma - {m^1}a + \left( {ma} \right) = T - mg + {m^1}g + mg - T \\
   \Rightarrow 2ma - {m^1}a = {m^1}g \\
   \Rightarrow {m^1}g + {m^1}a = 2ma \\
   \Rightarrow {m^1}\left( {g + a} \right) = 2ma \\
   \Rightarrow {m^1} = \dfrac{{2ma}}{{\left( {g + a} \right)}} \\
  \therefore {m^1} = \dfrac{{2ma}}{{a + g}} \\
 $
Therefore, the ballast mass to be released from the parachute to have an upward acceleration is $\dfrac{{2ma}}{{a + g}}$
Hence, the correct option is Option A.

Note:When you are adding two equations, then the LHS of one equation must be added to the LHS of another equation and the same with RHS too. Do not swap the places as the result may go wrong. Thrust pushes the parachute upwards by pushing the gases downwards in the opposite direction and gravitational force pulls the parachute downwards towards the centre of earth. Be careful with this.