Question

A number which divides 41 and 68 leaves 5 as a remainder. What is the number?

Answer 1

Hint: We have to use the concept of Highest common factor (HCF) i.e. number that can be divided exactly into each of two or more numbers. Then, we will subtract remainder from dividend and will find HCF of obtained numbers. It is written as $41-5=36$ and $68-5=63$ . Thus, finding HCF of 36, 63 we will get our number.

Complete step-by-step answer:
Here, we have to find a number which divides 41 and 68 and leaves remainder 5. Now, we will take example:
  

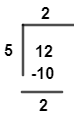
We can see that if remainder is subtracted from dividend i.e. 2 is subtracted from 12, then we get 10. Similarly, we will subtract5 from 41 and 68.
So, we will get $41-5=36$ and $68-5=63$ .
Now, we will find HCF of 36, 63 using the prime factorization method. So, we will get as
$36=2\times 2\times 3\times 3$
$36=3\times 3\times 7$
We can see that in both, $3\times 3$ is common. So, $3\times 3=9$ is our HCF.
Thus, 9 is the number when divided to 41 and 68 leaves remainder 5.

Note: This is a tricky question, so be careful while using HCF. Sometimes instead of HCF, students take LCM and try to solve this. LCM of 36, 63 is 252, so the number is 252 which is wrong. Always do verification while getting the final answer whether it is matching with the question or not. In this 41 divided by 252 gives answers in decimal form. So, understand the question first and then solve it.