Question

A normal is drawn at a point$S(x,y)$ of a curve. It meets the $x$-axis at$R$. If $SR$ is of constant length$\lambda $. If the curve passing through$(0,\lambda )$then its equation is
a)A circle with radius$\lambda $
b)An ellipse
c)A hyperbola
d)A parabola

Answer 1

Hint: Take a point on$R$and find the distance between$SR$and you will get two equations. Find the value of $(x-h)$ and substitute it. So integrate the two equations you will get the equation of the curve.

Complete step-by-step answer:

Now it is mentioned in the question that a normal is drawn at a point$S(x,y)$of a curve and meets $x$-axis at $R$. So you can see below we had assumed a curve, and a normal drawn at point$S(x,y)$.

So it is given in question that $l(SR)=\lambda $.

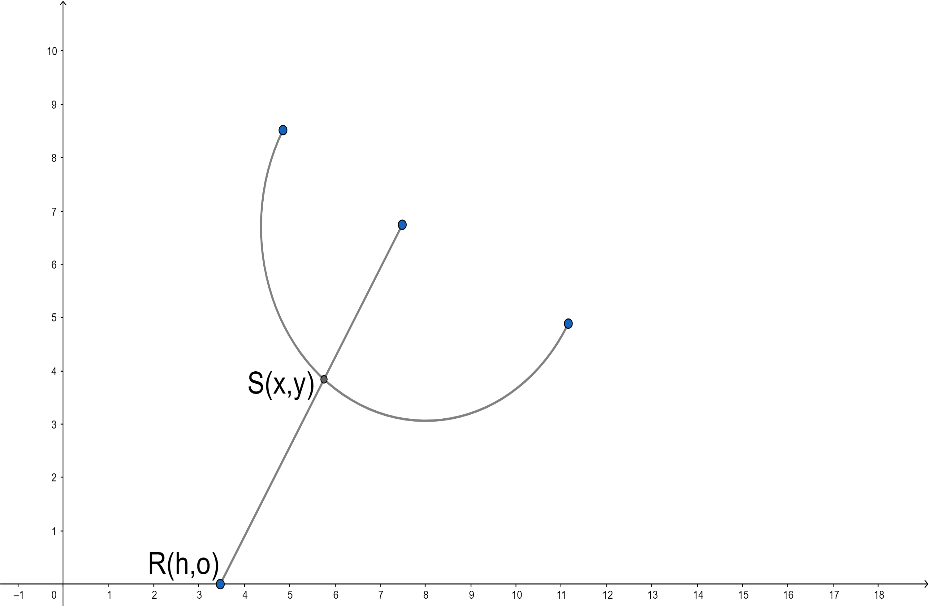
Now we have considered a point$R$on $x$-axis such that $R(h,0)$,

Now we have to find that the curve is of which type,

So, now we should find the distance of $SR,$ to find the distance of $SR$let us use distance formula,

 Given the two points$({{x}_{1}},{{y}_{1}})$and$({{x}_{2}},{{y}_{2}})$, the distance d between these points is given by the distance formula,

$d=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

They only indicate that there is a "first" point and a "second" point; that is, that you have two points. Whichever one you call "first" or "second" is up to you. The distance will be the same, regardless.

Using distance formula to find distance for$SR,$i.e., points are$(x,y)$and$(h,0)$, we get

\[d(SR)=\sqrt{{{(x-h)}^{2}}+{{(y-0)}^{2}}}\]

\[d(SR)=\sqrt{{{(x-h)}^{2}}+{{y}^{2}}}\]

So, substituting$l(SR)=d(SR)=\lambda $in above we get,

\[\lambda =\sqrt{{{(x-h)}^{2}}+{{y}^{2}}}\]

Squaring both sides we get,

\[{{\lambda }^{2}}={{(x-h)}^{2}}+{{y}^{2}}\]

Now rearranging we get,

\[{{(x-h)}^{2}}+{{y}^{2}}={{\lambda }^{2}}\] ………..(1)

Now let us find the value of$(x-h)$, from above equation we get the value of$(x-h)$,

\[(x-h)=\pm \sqrt{{{\lambda }^{2}}-{{y}^{2}}}\]………… (2)

Now differentiating equation (1) w.r.t $x$ we get,

$2(x-h)+2y{{y}^{'}}=0$

Now dividing above equation by $2$ we get,

$(x-h)+y{{y}^{'}}=0$

$(x-h)=-y{{y}^{'}}$

So, from equation (2), we get,

$\pm \sqrt{{{\lambda }^{2}}-{{y}^{2}}}=-y{{y}^{'}}$

So simplifying we get,

$\pm \sqrt{{{\lambda }^{2}}-{{y}^{2}}}=y{{y}^{'}}$

Now there are two conditions, i.e., $\sqrt{{{\lambda }^{2}}-{{y}^{2}}}=y{{y}^{'}}$ and
$-\sqrt{{{\lambda }^{2}}-{{y}^{2}}}=y{{y}^{'}}$,

Now consider,

$\sqrt{{{\lambda }^{2}}-{{y}^{2}}}=y{{y}^{'}}$

So putting integration on both sides, ${{y}^{'}}=\dfrac{dy}{dx}$ we get,

\[\begin{align}

  & \int{\sqrt{{{\lambda }^{2}}-{{y}^{2}}}}=\int{y\dfrac{dy}{dx}} \\

 & \int{\dfrac{y}{\sqrt{{{\lambda }^{2}}-{{y}^{2}}}}}dy=\int{dx} \\

\end{align}\]

Now simplifying we get,

\[-\dfrac{1}{2}\int{\dfrac{-2y}{\sqrt{{{\lambda }^{2}}-{{y}^{2}}}}}dy=\int{dx}\]

So, taking \[{{\lambda }^{2}}-{{y}^{2}}=t\], and differentiating we get,

\[-2ydy=dt\]

\[-\dfrac{1}{2}\int{\dfrac{dt}{\sqrt{t}}}=\int{dx}\] ………………(We

know$\int{\dfrac{1}{\sqrt{x}}}dx=2\left[ {{x}^{\dfrac{1}{2}}} \right]+c$)

So simplifying we get,

\[-\dfrac{1}{2}\left[ \dfrac{{{t}^{\dfrac{1}{2}}}}{\dfrac{1}{2}} \right]=x+c\]

\[-{{t}^{\dfrac{1}{2}}}=x+c\]

Now replacing value of $t$, we get,

\[-\sqrt{{{\lambda }^{2}}-{{y}^{2}}}=x+c\]

Now it is given, in question that it passes through $(0,\lambda )$, so substituting we get,

\[\begin{align}

  & -\sqrt{{{\lambda }^{2}}-{{\lambda }^{2}}}=0+c \\

 & c=0 \\

\end{align}\],

So we get the equation as,

\[-\sqrt{{{\lambda }^{2}}-{{y}^{2}}}=x\]

Squaring both sides we get,

\[{{\lambda }^{2}}-{{y}^{2}}={{x}^{2}}\]

Now rearranging we get,

\[{{x}^{2}}+{{y}^{2}}={{\lambda }^{2}}\] ………………. (2)

So now taking$-\sqrt{{{\lambda }^{2}}-{{y}^{2}}}=y{{y}^{'}}$

So integrating both sides, we get,

\[\begin{align}

  & -\int{\sqrt{{{\lambda }^{2}}-{{y}^{2}}}}=\int{y\dfrac{dy}{dx}} \\

 & -\int{\dfrac{y}{\sqrt{{{\lambda }^{2}}-{{y}^{2}}}}}dy=\int{dx} \\

\end{align}\]

So now simplifying we get,

\[\dfrac{1}{2}\int{\dfrac{-2y}{\sqrt{{{\lambda }^{2}}-{{y}^{2}}}}}dy=\int{dx}\]

So taking\[{{\lambda }^{2}}-{{y}^{2}}=t\], and differentiating we get,

\[-2ydy=dt\]

\[\dfrac{1}{2}\int{\dfrac{dt}{\sqrt{t}}}=\int{dx}\]

So simplifying we get,

\[\dfrac{1}{2}\left[ \dfrac{{{t}^{\dfrac{1}{2}}}}{\dfrac{1}{2}} \right]=x+c\]

\[{{t}^{\dfrac{1}{2}}}=x+c\]

Now replacing value of $t$, we get,

\[\sqrt{{{\lambda }^{2}}-{{y}^{2}}}=x+c\]

Now it is given, in question that it passes through$(0,\lambda )$.so substituting we get,

\[\begin{align}

  & \sqrt{{{\lambda }^{2}}-{{\lambda }^{2}}}=0+c \\

 & c=0 \\

\end{align}\],

We get the equation as,

\[\sqrt{{{\lambda }^{2}}-{{y}^{2}}}=x\]

Squaring both sides we get,

\[{{\lambda }^{2}}-{{y}^{2}}={{x}^{2}}\]

On rearranging we get,

\[{{x}^{2}}+{{y}^{2}}={{\lambda }^{2}}\] ………………. (3)

From (2) and (3), we get the same equation. The equation of curve as,

\[{{x}^{2}}+{{y}^{2}}={{\lambda }^{2}}\]

The equation we can see is the equation of the circle with radius $\lambda $.

So, we get the correct answer as option (a).


Note: Read the question carefully. Use distance formulas in the proper manner. Assumption of point $R$ is necessary. Be familiar with the integration. You should also know the integration. Also necessary substitution is done, don't confuse yourself while solving or integrating. After this \[\sqrt{{{\lambda }^{2}}-{{y}^{2}}}=x+c\] don’t forget to find the value of $c$, for that don’t forget to substitute $(0,\lambda )$.