Question

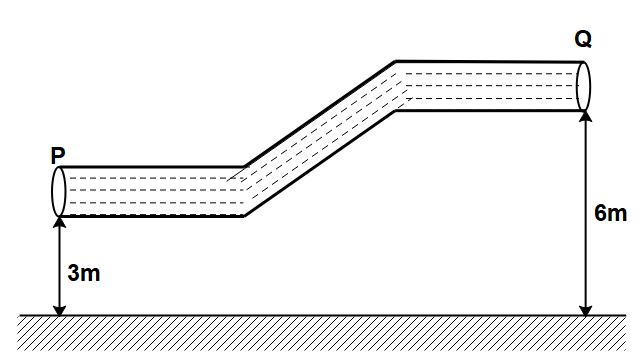
A non-viscous liquid of constant density $500kg/{m^3}$ flows in a variable cross-sectional tube. The area of cross-section of the tube at two points P and Q at heights of $3m$ and $6m$ are $2 \times {10^{ - 3}}{m^2}$ and $4 \times {10^{ - 3}}{m^2}$ respectively. The work done per unit volume by the forces of gravity as the fluid flows from point P to Q, is:

A. $29.4J/{m^3}$
B. $ - 1.47 \times {10^4}J/{m^3}$
C. $ - 2.94 \times {10^4}J/{m^3}$
D. none of these

Answer 1

Hint: To find the work done per unit volume by the forces of gravity, we can use Bernoulli's principle. Initially the height of the liquid is less, but we have increased the height. Thus, increasing the potential energy. So, in Bernoulli's principle the potential energy per unit volume of the liquid is the work done.

Formula used:
${W_g} = - \rho g\left( {{h_2} - {h_1}} \right)$

Complete step-by-step answer:
In the above question, they’ve given that a non-viscous fluid is flowing in a tube whose area of cross-section varies. They’ve asked us to find the work done per unit volume by the forces of gravity.
From Bernoulli’s equation we have,
${P_1} - {P_2} = \dfrac{1}{2}\rho \left( {v_2^2 - v_1^2} \right) + \rho g\left( {{h_2} - {h_1}} \right)$
Here,
${P_1} - {P_2}$ is the pressure energy density of the fluid
$\dfrac{1}{2}\rho \left( {v_2^2 - v_1^2} \right)$ is the kinetic energy density of the fluid
$\rho g\left( {{h_2} - {h_1}} \right)$ is the potential energy density of the fluid
In this problem we’re only concerned with the work done by gravity per unit volume which is the potential energy per unit volume of the fluid. It is given by
${W_g} = - \rho g\left( {{h_2} - {h_1}} \right)$
Where,
${W_g}$ is the work done by gravity per unit volume
$\rho $ is the density of the fluid
$g$ is the acceleration due to gravity
${h_2}$ and ${h_1}$ are the heights attained by the fluid
Here, the negative symbol indicates that we are doing the work against gravity by increasing its potential energy i.e., the gravity is pulling the fluid towards earth but we’re doing work (by applying force) in the opposite direction.
$\eqalign{
  & {W_g} = - \rho g\left( {{h_Q} - {h_P}} \right) \cr
  & \Rightarrow {W_g} = - 500kg/{m^3} \times 9.8m/{s^2} \times \left( {6m - 3m} \right) \cr
  & \Rightarrow {W_g} = - \left( {4900 \times 3} \right)J/{m^3} = - 14700J/{m^3} \cr
  & \therefore {W_g} = - 1.47 \times {10^4}J/{m^3} \cr} $
Thus, the work done by gravity per unit volume is ${W_g} = - 1.47 \times {10^4}J/{m^3}$.

So, the correct answer is “Option B”.

Note: You can notice, in the question that, the area and velocity of the fluid are also given. With the help of these, we can find the kinetic energy density of the fluid. Here, the energy density is nothing but the energy per unit volume of the fluid.
In the problem, we’ve interchangeably used the word fluid and liquid. It is because Bernoulli's principle applies to all fluids. And the fluids are mainly categorized into liquids, gases and plasma, though we primarily deal only with liquids and gases.