Question

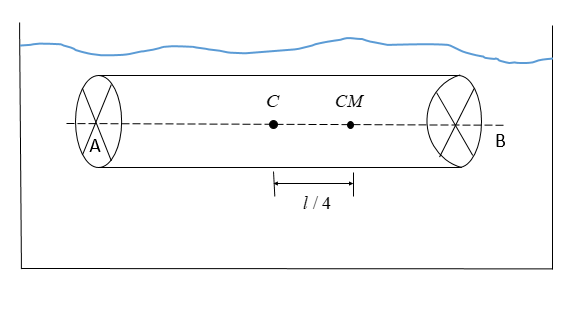
A non-uniform cylinder of mass m, length and radius r is having its centre of mass at a distance l from the centre and lying on the axis of the cylinder. the cylinder is kept in a liquid of uniform density p. the moment of inertia of the rod about the centre of mass is $I$. the angular acceleration of point A relative to point B just after the rod is released from the position as shown in the figure is

A. $\dfrac{\pi \rho g{{l}^{2}}{{r}^{2}}}{I}$
B. $\dfrac{\pi \rho g{{l}^{2}}{{r}^{2}}}{4I}$
C. $\dfrac{\pi \rho g{{l}^{2}}{{r}^{2}}}{2I}$
D. $\dfrac{3\pi \rho g{{l}^{2}}{{r}^{2}}}{4I}$

Answer 1

Hint: Angular acceleration can be easily found using the torque equation. Firstly, find all the forces acting on the body. Using these forces find the torque produced by these forces. Then, use the torque equation for all the torques combined taking the appropriate point as origin.

Formula used:
$I\alpha =\sum\limits_{i=1}^{n}{({{F}_{i}}{{l}_{i}})}$

Complete step by step answer:
In the body submerged into the fluid, there are two forces acting upon it simultaneously. These two forces are buoyant force and gravitational force.
Buoyant force is an upward force, applied by the fluid, whenever a body is submerged into that fluid. Buoyant force always acts at the geometrical centre of the body.
Buoyant force can be expressed as $V\rho g$
Here, buoyant force on the cylinder = $V\rho g$ ----(i)
We know, volume of a cylinder = $\pi {{r}^{2}}l$
Hence, buoyant force on the cylinder = $\pi {{r}^{2}}l\rho g$=${{F}_{1}}$ ----(ii)
This buoyant force acts at the centre of the body, i.e., at point A
Also, the gravitational force is nothing but the weight of the body. Gravitational force is going to act at the centre of mass of the body. Here, the centre of mass is at point B.
So, Gravitational Force = $mg$= ${{F}_{2}}$ ----(iii)
The above forces are acting on the body as follows:

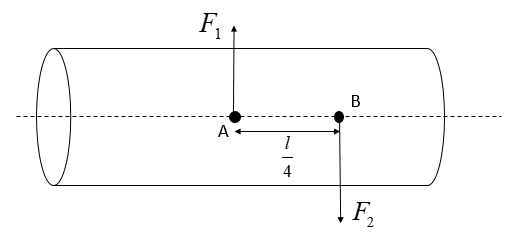
We need to find the angular acceleration of point A w.r.t. point B. So, let us consider point B as origin.
The torque equation can be written as:
$I\alpha ={{F}_{1}}\times \dfrac{l}{4}+{{F}_{2}}\times 0$
$\Rightarrow \alpha =\dfrac{{{F}_{1}}l}{4I}$
$\Rightarrow \alpha =\dfrac{\pi {{r}^{2}}{{l}^{2}}\rho g}{4I}$
Hence the angular acceleration of point A relative to point B just after the rod is released is $\alpha =\dfrac{\pi {{r}^{2}}{{l}^{2}}\rho g}{4I}$

So, the correct answer is “Option B”.

Note:
To find the angular acceleration of a body, firstly find all the forces acting on that body. These forces acting at different parts of the body produce torque. The net torque may or may not be zero. Use the torque equation to find the angular acceleration of the body. If net torque is zero, angular acceleration will become zero.