Question

A non-conducting sphere of radius $ A $ has net charge $ + q $ uniformly distributed throughout in volume. A hollow spherical conductor having inner and outer, radii ' $ b $ ' and ' $ c $ ' and net charge ' $ - q $ ' is concentric with the sphere (see the figure) Read the following statements:

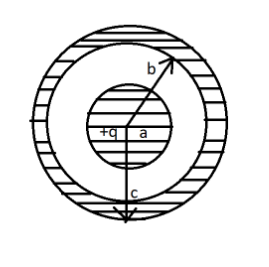
(i) The electric field at a distance $ {{r}} $ from the centre of the sphere $ = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{{qr}}}}{{{{{a}}^3}}} $ for $ {{r}} < {{a}} $
(ii) The electric field at distance $ {{r}} $ from the centre of the sphere for $ {{a}} < {{r}} < {{b}} = 0 $
(iii) The electric field at distance $ {{r}} $ from the centre of the sphere for $ {{b}} < {{r}} < {{c}} = 0 $
(iv) The charge on the inner surface of the hollow sphere $ = - {{q}} $
(v) The charge on the outer surface of the hollow sphere $ = + {{q}} $
Which of the above statements are true?
(A) (i.), (ii.) and (v.)
(B) (i.), (iii.) and (iv.)
(C) (ii.), (iii.), and (iv).
(D) (ii.), (iii.), and (v.)

Answer 1

Hint: It is possible to consider the electric field as an electrical property associated with each point in the space where a charge is present in any form. The electric force per unit charge is also described as an electric field.

Complete Step-by-Step Solution
Let $ {{{q}}^1} $ is the inner surface charge.
Then, $ {q_{outer}} = - q - {q^1} $
 $ {{{q}}_{{{inside}}}}{{ + }}{{{q}}_{{{outside}}}} = - q $
Electric field inside
The conductor should be zero $ (r > b $ and $ r < e) $ so in the arbitrary Gaussian surface
Electric flux $ = \dfrac{{{{ }}{{{q}}_{{{inside}}}}{{ }}}}{{{\varepsilon _0}}} = 0 $
 $ \Rightarrow $ $ {{ }}{{{q}}_{{{inside}}}} $ $ ({{b}} < {{r}} < {{c}}) = {{{q}}^1} + {{q}} = 0 $
 $ {{{q}}^1} = - {{q}} $
So, $ {{ }}{{{q}}_{{{inside}}}} $ $ = - {{q}} $ and $ {{{q}}_{{{outer }}}} = 0 $
Electric field for $ r < a $ is,
 $ {{E}} \times 4\pi {{{r}}^2} = \dfrac{{{{ }}{{{q}}_{{{inside}}}}{{ }}}}{{{\varepsilon _0}}} $
As a charge is uniformly distributed $ q $ inside $ = \left( {\dfrac{{{r^3}}}{{{a^3}}}} \right)q $
So, $ {{E}} \times 4\pi {{{r}}^2} = \dfrac{{{{{r}}^3}{{q}}}}{{{{{a}}^3}{\varepsilon _0}}} $
 $ \Rightarrow {{E}} = \dfrac{1}{{4\pi }} \times \dfrac{{{q}}}{{{{{a}}^3}{\varepsilon _0}}} $
Now, electric field for $ {{a}} < {{r}} < {{b}} $ ,
 $ {{E}} = \dfrac{{{{kq}}}}{{{{{r}}^2}}} $
Now, the electric field for $ {{b}} < {{r}} < {{c}} $
As told earlier, $ {{E}} = {{O}} $
Now, the electric field for $ {{c}} < {{r}} $
 $ {{E}} = \dfrac{{{{{k}}_{{{quotes}}}}}}{{{{{r}}^2}}} = {{k}}\dfrac{{{{(0)}^2}}}{{{{{r}}^2}}} = 0 $
Hence, the correct option is (C).

Note
Mathematically, the electric field is defined as a vector field that can be associated with each point in space, at which point the force per unit charge is exerted on a positive test charge at rest. The electric field is generated by electric charges or by magnetic fields that vary in time. The electric field is responsible for the attractive forces between the atomic nucleus and the electrons that then hold together in the case of the atomic scale.