Question

A nine similar resistors of resistance R are connected as shown in the figure. Find the equivalent resistance between points A and B.
                            

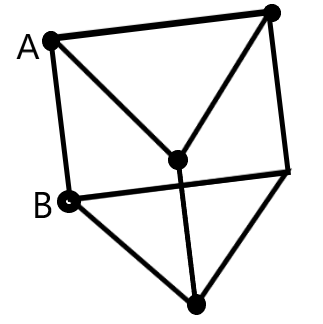
Answer 1

Hint: We are given a combination of resistances. We have to resolve them as in series or as in parallel to find the equivalent resistance of the circuit across the points A and B. We can resolve them easily by identifying the circuit closely.

Complete answer:
We need to resolve the resistors to understand whether they are in series or parallel to each other. Let us get a clearer idea of the network as –
           

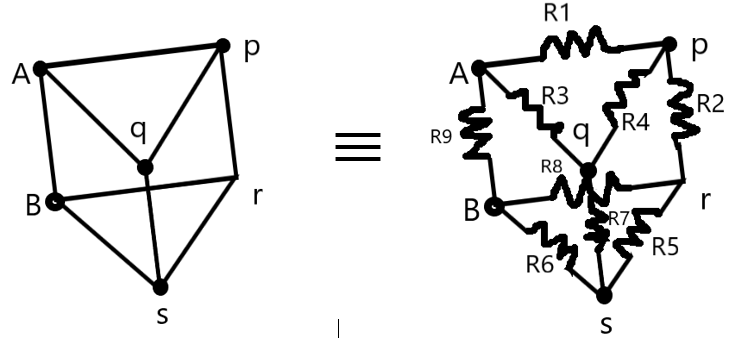
We can elaborate the connections as shown in the above diagram.
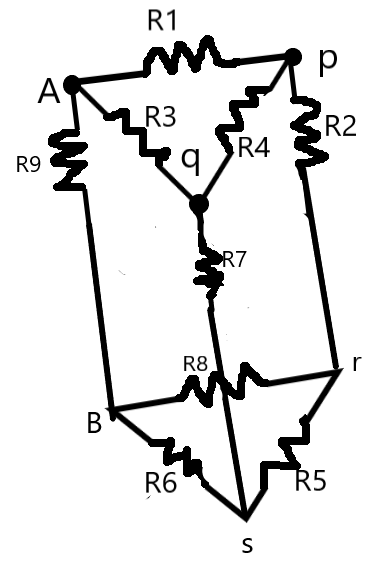
A closer approach to circuit will help us find two pairs of equipotential points in the circuit. From the Wheatstone’s bridge condition, we know that, a resistor in between two equipotential points due not play a role in the circuit, i.e., there will be no potential drop or current flow across these resistors.
The points p and q on the left arm of the circuit are at equal potentials as a result, the current through R4 is zero and thus, we can neglect the resistance R4.
Similarly, the points r and s are also at equal potentials, i.e., we can neglect the resistor R5. We get the resultant circuit as –
                         

.
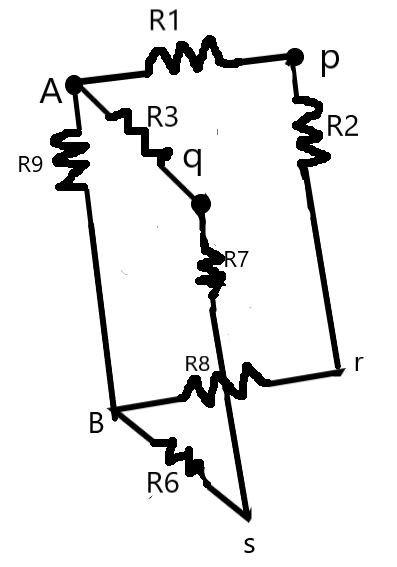Now, we can find that the resistances (R1, R2, R8), (R3, R7, R6) are pairs of series resistors parallel to each other and to R9.
We can compute the equivalent resistance as –
\[\begin{align}
  & {{R}_{s1}}=R1+R2+R8=3R \\
 & {{R}_{s2}}=R3+R7+R6=3R \\
 & \text{Now, R9 }\!\!|\!\!\text{ }\!\!|\!\!\text{ }{{\text{R}}_{s1}}||{{R}_{s2}}, \\
 & \Rightarrow \text{ }\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{R}+\dfrac{1}{3R}+\dfrac{1}{3R} \\
 & \Rightarrow \text{ }\dfrac{1}{{{R}_{eq}}}=\dfrac{5}{3R} \\
 & \therefore \text{ }{{R}_{eq}}=\dfrac{3R}{5}\Omega \\
\end{align}\]
The required equivalent resistance across A and B is \[\dfrac{3R}{5}\Omega \].

Note:
The Wheatstone’s bridge condition is very helpful in resolving many series-parallel circuits, as there will be mostly equipotential nodes in the circuit which will add error to the theoretical calculations by involving additional resistance in the circuit.