Question

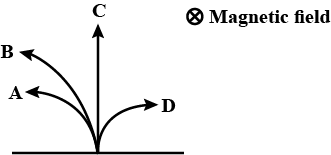
A neutron, a proton, an electron and an α-particle enter a region of uniform magnetic field with the same velocities. The magnetic field is perpendicular and directed into the plane of the paper. The tracks of particles are labelled in the figure. The electron follows the track?

Answer 1

Hint: The direction in which any charged particle moving with a certain velocity in a constant magnetic field will move can be given by Lorentz force. This direction is calculated by finding the vector cross product of the velocity of the charged particle and magnetic field and then multiplying the resulting term with the charge particle.

Complete step by step answer:
Mathematically, the equation of Lorentz force can be written as:
$\Rightarrow \overrightarrow{F}=q(\overrightarrow{v}\times \overrightarrow{B})$
Here we have,
$\overrightarrow{F}$ is the direction of force on the charged particle.
$q$ is the charge.
$\overrightarrow{v}$ is the velocity of the charge particle just before entering the magnetic field.
$\overrightarrow{B}$ is the applied magnetic field.
Now, when an electron enters the magnetic field we have:
The direction of the vector product $(\overrightarrow{v}\times \overrightarrow{B})$ is towards the left. Now, we multiply it with the charge of an electron which is negative. Hence the net force acting on the electron is now towards right.
This implies that, just after entering the magnetic field the electron starts moving towards right. And from our diagram, the only path towards right is path D.
Hence, path D is the path taken by the electron under the given magnetic field.
Also, for other charges we have:
The charge on a neutron is zero. Hence, the whole term becomes zero when no force is applied on it. Therefore, a neutron will traverse undeviated from its path.
In the case of protons and α-particles, we know that their initial velocities are the same as that of the electron. But the signs of their charges are opposite. Hence, these positively charged particles will move towards the left.

Note: It should be noted that, in the equation of Lorentz force while multiplying charge to the vector product of velocity and magnetic field, it is of utmost importance to take the sign of electric charge into consideration for both the types of charges, the direction of force will be opposite and not same.