Question

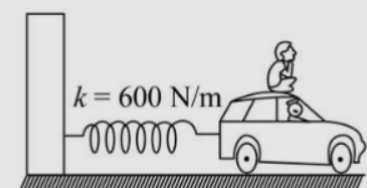
A naughty boy is sitting on the roof of a flat toy car of mass \[6\;{\rm{kg}}\]. If no slipping takes place between car and the boy then what should be the mass of the child in order to have a period of system equal to \[0.758\;\sec \] ?

A. \[2.74\;{\rm{kg}}\]
B. \[6\;{\rm{kg}}\]
C. \[3\;{\rm{kg}}\]
D. None of these

Answer 1

Hint: The above problem can be resolved using the fundamental concepts and the mathematical formula for the time period of a spring-loaded system. In this problem, a car of defined mass is given with a child sitting in the car. Then we can apply the formula for the time period. As the numerical value for the time period is given to us, we simply substitute the values in the formula, such that we can obtain the value of the mass of the child sitting on the toy car.

Complete step by step answer:
Given:
The mass of the toy car is, \[m = 6\;{\rm{kg}}\].
The time period of the system is, \[T = 0.758\;{\rm{sec}}\].
The spring constant from the figure is, \[K = 600\;{\rm{N/m}}\].
The mathematical formula for the time period of the system is,
\[T = 2\pi \sqrt {\dfrac{{m + M}}{K}} \]
Here, M is the mass of the Child.
Solve by substituting the value in above expression as,
\[
T = 2\pi \sqrt {\dfrac{{m + M}}{K}} \\
\Rightarrow 0.758\;{\rm{s}} = 2\pi \sqrt {\dfrac{{6\;{\rm{kg}} + M}}{{600\;{\rm{N/m}}}}}
\]
 Solve by squaring the both sides of above equation as,
\[
\Rightarrow {\left( {0.758\;{\rm{s}}} \right)^2} = {\left( {2\pi \sqrt {\dfrac{{6\;{\rm{kg}} + M}}{{600\;{\rm{N/m}}}}} } \right)^2}\\
\Rightarrow M = \dfrac{{{{\left( {0.758\;{\rm{s}}} \right)}^2} \times 600\;{\rm{N/m}}}}{{{{\left( {2\pi } \right)}^2}}} - 6\;{\rm{kg}}\\
\Rightarrow M \approx 2.74\;{\rm{kg}}
\]

Therefore, the mass of the child is \[2.74\;{\rm{kg}}\] and option (A) is correct.

Note:
To solve the given problem, one must be aware of the concepts that can be applied to analysing the spring-mass system. In a spring-mass system, the first variable to make sense is the spring constant. The spring constant or the spring stiffness constant is that parameter that decides the strength of the material of the spring. Moreover, the next to keep in mind is about the mass of the system, whether the mass of the total system or mass of a specific entity considered.