Question

A motorcyclist wants to drive on the vertical surface of a wooden well of radius 5m, with a minimum speed of $5\sqrt{5}m{{s}^{-1}}$. The minimum value of coefficient of friction between the tyres and the wall of the must be:
A. 0.10
B. 0.20
C. 0.30
D. 0.40

Answer 1

Hint: As a first step, you could depict the given condition in a diagram marking all the forces acting on the body. Thus, you will get a clear idea of the problem. Now, you would see that the normal force equal to the centripetal force and thus can be substituted in the equation for frictional force and then rearrange to get the answer.

Formula used:
Centripetal force,
${{F}_{c}}=\dfrac{m{{v}^{2}}}{r}$
Frictional force,
$f=\mu N$

Complete answer:
In the question, we are given a motorcyclist who wants to drive with a minimum speed of $5\sqrt{5}m{{s}^{-1}}$ on the vertical surface of the wooden well of radius 5m. We are asked to find the minimum value of coefficient of friction between the tyres and wall using these given observations.
First of all, let us depict the given situation in a diagram with all the forces on it marked.

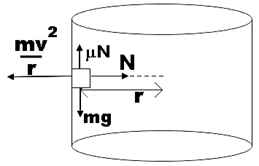
The motorcyclist is moving around the wall of the well so it will suffer from centripetal force which would be equal to the normal force, that is,
$N=\dfrac{m{{v}^{2}}}{r}$ ……………………………….. (1)
We know that it is the frictional force that is acting against gravity to prevent the motorcyclist from falling into the well, so,
$\mu N=mg$
Substituting (1), we get,
$\mu \left( \dfrac{m{{v}^{2}}}{r} \right)=mg$
$\Rightarrow \mu =\dfrac{gr}{{{v}^{2}}}$
But,
$r=5m$
$v=5\sqrt{5}m{{s}^{-1}}$
Substituting these values,
$\mu =\dfrac{10\times 5}{{{\left( 5\sqrt{5} \right)}^{2}}}$
$\Rightarrow \mu =\dfrac{50}{25\times 5}=\dfrac{10}{25}$
$\therefore \mu =0.04$
Therefore, we found the minimum value of coefficient of friction between the tyres and the wall to be 0.04.

Hence, option D is found to be the correct answer.

Note:
If the motorcyclist had been moving on a horizontal surface the normal force would have been equal to the weight of the body. But here the motion is very different. And the frictional force is known to oppose the relative motion, but here it holds the motorbike from falling into the well thus it is opposing a possible motion here.