Question

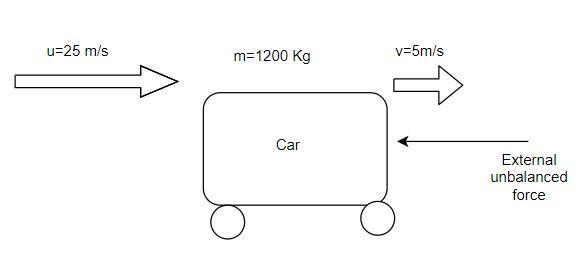
A motorcar of mass $1200\,Kg$ is moving along a straight line with a uniform velocity of $90\,Km{h^{ - 1}}$. Its velocity is slowed down to $18\,Km{h^{ - 1}}$ in $4\,s$ by an unbalanced external force. Calculate the acceleration and change in momentum. Also calculate the magnitude of the force required.

Answer 1

Hint
By using the formula of change in momentum calculate its value. By using the formula given, substitute the values and calculate the acceleration of the car when it is stopped by the unbalanced external force. From this value, calculate the force by using the formula of law of motion.
(1) The change in the momentum is given by
$\Rightarrow \Delta P = mv - mu$
Where $\Delta P$ is the rate of change of momentum, $mv$ is the final momentum and the $mu$ is the initial momentum.
(2) Final velocity is given by
$\Rightarrow v = u + at$
Where $v$ is the final velocity, $u$ is the initial velocity, $a$ is the acceleration of the car and the $t$ is the time taken.
(3) Newton’s second law
$\Rightarrow F = ma$
Where $F$ is the force exerted by the car and $m$ is the mass of the car.

Complete step by step answer
The given data are
Mass of the motorcar, $m = 1200\,Kg$
Initial velocity, $u = 90\,km{h^{ - 1}}$
$\Rightarrow u = 25\,m{s^{ - 1}}$
The final velocity, $v = 18\,Km{h^{ - 1}} = 5m{s^{ - 1}}$
The time taken by the car to travel, $t = 4\,s$

By using the change in momentum formula,
$\Rightarrow \Delta P = mv - mu$
$\Rightarrow \Delta P = m\left( {v - u} \right)$
$\Rightarrow \Delta P = 1200\left( {25 - 5} \right)$
By doing the simple arithmetic operation
$\Rightarrow \Delta P = - 24000\,Kgm{s^{ - 1}}$
The change in momentum is negative since the car slows down by the external force.
By using the formula (2) to calculate the acceleration.
$\Rightarrow v = u + at$
$\Rightarrow 5 = 25 + \left( {a \times 4} \right)$
By simplifying the above equation,
$\Rightarrow 5 - 20 = a \times 4$
$\Rightarrow a = - 5\,m{s^{ - 2}}$
The acceleration of the car is $ - 5\,m{s^{ - 2}}$ and hence its retards the motion of the car.
By using the formula (3),
$\Rightarrow F = ma$
$\Rightarrow F = 1200 \times - 5$
$\Rightarrow F = - 6000\,N$, since the magnitude of the force is alone questioned not the direction,
$\Rightarrow \left| F \right| = \left| { - 6000} \right|$
$\Rightarrow F = 6000\,N$
Hence the magnitude of the force exerted is $6000\,N$.

Note
The units given must be converted into standard units. This can be done by using $1\,Km{h^{ - 1}} = \dfrac{5}{{18}}\,m{s^{ - 1}}$. If the balanced force is applied in place of the unbalanced force, the car stops suddenly without any retarded acceleration. Thus unbalanced force lowers the car's acceleration slowly and this continues and the car stops.