
A motorboat is observed to travel $10km{{h}^{-1}}$ relative to the earth in the direction ${{37}^{\circ }}$ north of east. If the velocity of the boat due to the wind only is $2km{{h}^{-1}}$ westward and that due to the current only is $4km{{h}^{-1}}$ southward, what is the magnitude and direction of the velocity of the boat due to its own power?
Answer
572.1k+ views
Hint: First draw a schematic diagram showing the data given in the question. The component of velocity in the north of east is resolved into two components. That is, the cosine component along the horizontal direction and the vertical component along vertical direction. Then calculate the resultant velocity in the horizontal and vertical direction and then find the net velocity.
Complete answer:
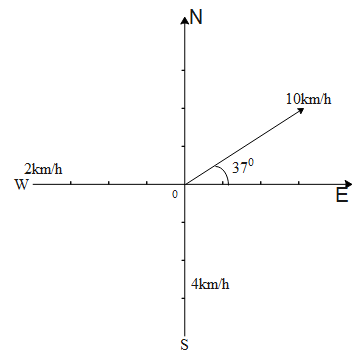
Since the motorboat travels $10km{{h}^{-1}}$relative to the earth in the direction ${{37}^{\circ }}$north of east. The velocity component splits into horizontal and vertical components here. This is shown in the figure below.
$10\cos {{37}^{\circ }}=7.896\simeq 8km/h$
$10\sin {{37}^{\circ }}=6.018km/h\simeq 6km/h$
Then the vertical velocity $=6-4=2km{{h}^{-1}}$
Similarly,
The horizontal velocity$=8-2=6km{{h}^{-1}}$
Thus net velocity can be described as the square of the horizontal and vertical velocity.
Hence, the net velocity,
$\begin{align}
& {{V}_{net}}=\sqrt{{{2}^{2}}+{{6}^{2}}} \\
& \\
\end{align}$
$\begin{align}
& \Rightarrow {{V}_{net}}=\sqrt{4+36} \\
& \Rightarrow {{V}_{net}}=\sqrt{40} \\
& \therefore {{V}_{net}}=2\sqrt{10}km{{h}^{-1}} \\
\end{align}$
Additional information:
The motion of one object with respect to the other is known as a relative motion. Here one object is assumed to be fixed while the other is in relative motion. Thus net velocity can be described as the square of the horizontal and vertical velocity.
Note:
The motion of one object with respect to the other is known as a relative motion. Here one object is assumed to be fixed while the other is in relative motion. For any vector we can resolve them into two components. That is, horizontal and vertical components. The horizontal component is usually taken as sine component and vertical component is taken as cosine. Thus net velocity can be described as the square of the horizontal and vertical velocity.
Complete answer:

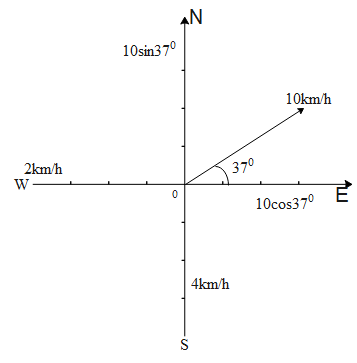
Since the motorboat travels $10km{{h}^{-1}}$relative to the earth in the direction ${{37}^{\circ }}$north of east. The velocity component splits into horizontal and vertical components here. This is shown in the figure below.

$10\cos {{37}^{\circ }}=7.896\simeq 8km/h$
$10\sin {{37}^{\circ }}=6.018km/h\simeq 6km/h$
Then the vertical velocity $=6-4=2km{{h}^{-1}}$
Similarly,
The horizontal velocity$=8-2=6km{{h}^{-1}}$
Thus net velocity can be described as the square of the horizontal and vertical velocity.
Hence, the net velocity,
$\begin{align}
& {{V}_{net}}=\sqrt{{{2}^{2}}+{{6}^{2}}} \\
& \\
\end{align}$
$\begin{align}
& \Rightarrow {{V}_{net}}=\sqrt{4+36} \\
& \Rightarrow {{V}_{net}}=\sqrt{40} \\
& \therefore {{V}_{net}}=2\sqrt{10}km{{h}^{-1}} \\
\end{align}$
Additional information:
The motion of one object with respect to the other is known as a relative motion. Here one object is assumed to be fixed while the other is in relative motion. Thus net velocity can be described as the square of the horizontal and vertical velocity.
Note:
The motion of one object with respect to the other is known as a relative motion. Here one object is assumed to be fixed while the other is in relative motion. For any vector we can resolve them into two components. That is, horizontal and vertical components. The horizontal component is usually taken as sine component and vertical component is taken as cosine. Thus net velocity can be described as the square of the horizontal and vertical velocity.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




