Question

A motorboat going downstream overcame a raft at a point A; $ \tau = 60\min $ later it turned back and after some time the raft was at a distance $ l = 6km $ from the point $ A $ . Find the flow velocity in $ km{h^{ - 1}} $ assuming the duty of the engine to be constant.
 $\left( A \right)3km{h^{ - 1}} \\
  \left( B \right)1km{h^{ - 1}} \\
  \left( C \right)5km{h^{ - 1}} \\
  \left( D \right)6km{h^{ - 1}} \\ $

Answer 1

Hint :In order to solve this question, we are going to first analyze the motion of the boat down the stream and its velocity at the various points of the motion, then, by forming the equation of motion for the velocity of the boat and on solving and simplifying the equation, we get the value of $ {v_0} $ .

Complete Step By Step Answer:
Let us consider the motion of the boat down the stream as given in the question. The figure that can be drawn for the motion is

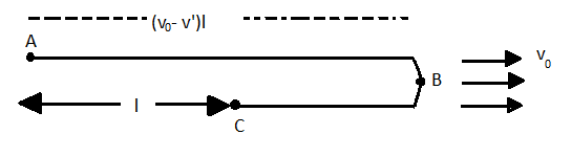
Let us consider $ {v_0} $ to be the stream velocity and the velocity of the boat with respect to the water be $ v' $ . Here the boat reached at a point B while going downstream with the velocity $ \left( {{v_0} + v'} \right) $ and then returned with the velocity $ \left( {v' - {v_0}} \right) $ and then, the raft passed the point C.
Let the time taken by the raft to reach the point from A to C be $ t $ , for the time the boat reaches first from the point A to the point B and then from the point B to C.
Therefore, the equation formed by the velocities be
 $ \dfrac{1}{{{v_0}}} = \tau + \dfrac{{\left( {{v_0} + v'} \right)\tau - 1}}{{\left( {v' - {v_0}} \right)}} $
On solving this equation for the value of $ {v_0} $
Thus, we get
 $ {v_0} = \dfrac{1}{{2\tau }} $
Now, putting the value of $ \tau $ , we get
 $ {v_0} = 3km{h^{ - 1}} $

Note :
In downstream motion, the speed of the boat is equal to the sum of the speed of boat in still water and the speed of river water while in the upstream motion, the speed of the boat is equal to the difference of the speed of boat in still water and the speed of river water.