Question

A monkey is sitting at a height of 5m on a tree. There is fruit on the ground at a distance of 10m from the fruit of the tree. The money gets down and goes straight towards the fruit. If instead it would have climbed up to the top of the tree and from there jumped at the fruit the distance traveled would have been the same as before. Find the height of the tree.

Answer 1

Hint: First find the distance when the monkey gets down and goes towards the tree and then set it equal to the distance when the monkey climbed up to the top of the tree and then jumped at the fruit. After that solve the equation that gives the required result.

Complete step-by-step answer:
It is given that the monkey is sitting at height of 5m on a tree and the fruit is located at the distance of 10 m from the foot of the tree.
First monkey gets down from the tree and he is sitting at the height of $5$ m, so the covered distance is 5m and then he goes towards the fruit which is located at the distance of 10m from the foot of the tree, so the covered distance is 10 m. So, the total covered distance when the monkey gets down and goes towards the fruit is given as:
Covered distance is $\left( {5 + 10 = 15{\text{m}}} \right)$.

Now, assume that the height of the tree is $x$ then the figure of the problem is given as:

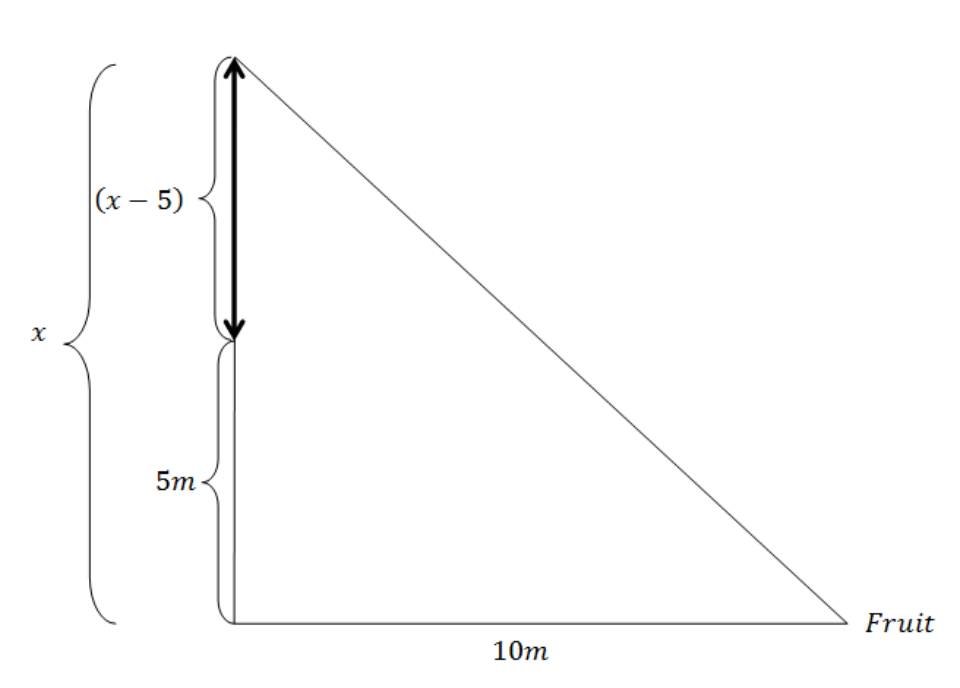
The distance of the fruit from the top of the tree is given using the Pythagoras theorem. The Pythagoras theorem says that:
Hypotenuse$ = \sqrt {{{\left( {{\text{perpendicular}}} \right)}^2} + {{\left( {{\text{base}}} \right)}^2}} $
Substitute the $x$ as the perpendicular, which is the height of the tree and $10$ as the base which is the distance of the fruit from the foot of the tree.
Distance$ = \sqrt {{x^2} + {{\left( {10} \right)}^2}} $
Distance$ = \sqrt {{x^2} + 100} $
When the monkey climbs on the top of the tree and then jump, then the covered distance is given as:
$ = \left( {x - 5} \right) + \sqrt {{x^2} + 100} $
It is given that in both the cases the distance traveled is the same, then
$
   \Rightarrow \left( {x - 5} \right) + \sqrt {{x^2} + 100} = 15 \\
   \Rightarrow \sqrt {{x^2} + 100} = 15 - x + 5 \\
   \Rightarrow \sqrt {{x^2} + 100} = 20 - x \\
$
Squaring both sides:
$ {\left( {\sqrt {{x^2} + 100} } \right)^2} = {\left( {20 - x} \right)^2} \\
   \Rightarrow {x^2} + 100 = {20^2} + {x^2} - 40x \\
   \Rightarrow 100 = 400 - 40x \\
$
$ \Rightarrow 40x = 400 - 100 \\
   \Rightarrow 40x = 300 \\
   \Rightarrow x = \dfrac{{30}}{4} = 7.5 \\
$

Therefore, the height of the tree is $7.5$ m. So, the correct option is (b).

Note: It is clear that the tree makes the angle of $90^\circ $ with the ground, therefore we can apply the Pythagoras theorem to find the hypotenuse of the formed triangle, which defines the distance of the fruit from the top of the tree.