Question

A miniature golf course is in the shape of an ellipse. The teeing off point and cup are located at foci 14 feet apart. The minor axis of the ellipse is 8 ft. long. If on the first shot a player hits the ball off to either side of the ground, the ball rolls and hits the boundary, bouncing off and proceeding to the cup. How much distance will the ball travel?

Answer 1

Hint: We use the basic definition and facts of the ellipse having standard equations to solve this question. We will use the relation between a, b and c that is given by ${c^2} = {a^2} - {b^2}$.

Complete step-by-step answer:

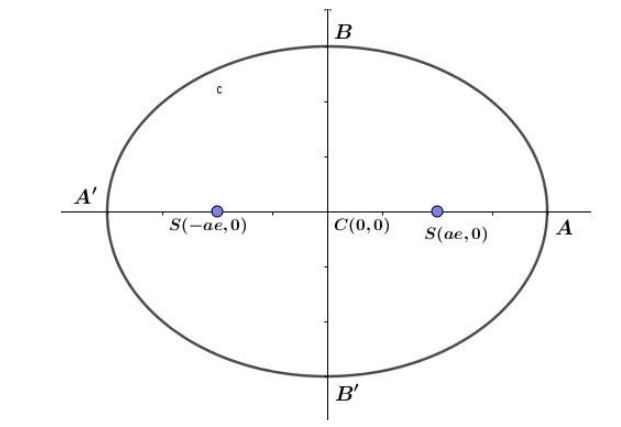
Let $S'( - ae,0)$ be the teeing off point and $S(ae,0)$be the cup point. Let $C(0,0)$ be the centre as shown in figure. Also let AA’ and BB’ be the major and minor axis respectively.
Thus we have,
$SS' = 2ae = 14ft.$ ,$CA = a$ and$CS = a - ae$
Now $CB = 8ft.$ (given)
If the player hits the ball from S’ and the ball hits the boundary A and cups to S as shown in figure.
$\therefore $ Total distance covered by ball $\begin{gathered}
   = S'C + CA + AS \\
   = ae + a + (a - ae) \\
   = 2a \\
\end{gathered} $
As we know that by basic definition of ellipse
$\begin{gathered}
  C{A^2} = C{B^2} - C{S^2} \\
  {a^2} = {8^2} + {7^2} = 113 \\
\end{gathered} $
$\therefore a = \sqrt {113} $
Thus, total distance covered by ball =$2a = 2\sqrt {113} $

Note: The set of all points in a plane, the sum of whose distances from two fixed points in the plane is constant, is an ellipse. These two fixed points are the foci of the ellipse. When a line segment is drawn joining the two focus points, then the mid-point of this line is the centre of the ellipse.
The line joining the two foci is called the major axis and a line drawn through the centre and perpendicular to the major axis is the minor axis. The endpoints of the major axis are called vertices of the ellipse