Question

A milk vendor has 2 cans of milk. The first container 25% water and rest milk. The second contains 50% water. How much milk should be mixed from each of the containers so as to get 12 litres of milk such that the ratio of water to milk is 3:5?

Answer 1

Hint:
Consider 1 litre of milk’s cost to be Re. 1. Thus find the cost price of 1 litre mix in the 1st can and the 2nd can. Find the mean price and find the ratio by the rules of alligation.

Complete step-by-step answer:
Let us assume the cost of 1 litre milk to be Re. 1.

Now the milk in 1 litre mix in the 1st can is equal to \[{}^{3}/{}_{4}\] litre.

Out of 1 litre 25% is \[{{{}^{3}/{}_{4}}^{th}}\] of the 1st can will be \[={}^{3}/{}_{4}\times \operatorname{Re}.1=\operatorname{Re}.{}^{3}/{}_{4}\].

Now let us consider the 2nd can.

The milk in 1 litre mix in 2nd can contains 50% of water, i.e. \[{}^{1}/{}_{2}\].

Milk in 1 litre mixin 2nd can = \[{}^{1}/{}_{2}\] litre.

Thus the cost price of 1 litre mix in the 2nd can = Re. \[{}^{1}/{}_{2}\].

The milk in 1 litre of final mix \[=\left( \dfrac{{}^{3}/{}_{4}+{}^{1}/{}_{2}}{2} \right)={}^{5}/{}_{8}\].

Thus the mean price = Re. \[{}^{5}/{}_{8}\].

By the rule of alligation, when different quantities of different ingredients are mixed together to produce a mixture of a mean value, the ratio of their quantities is inversely proportional to the difference in their cost from the mean value.

Thus by rule of alligation, we have \[{}^{x}/{}_{y}\].

\[\dfrac{x}{y}=\dfrac{CP\text{ }of\text{ }1\text{ }litre\text{ }mix\text{ }in\text{ }the\text{

}{{1}^{st}}can-Mean\text{ }price}{Mean\text{ }price-CP\text{ }of\text{ }1\text{ }litre\text{

}mix\text{ }in\text{ }the\text{ }{{2}^{nd}}can}\]

\[\dfrac{x}{y}=\dfrac{{}^{3}/{}_{4}-{}^{5}/{}_{8}}{{}^{5}/{}_{8}-{}^{1}/{}_{2}}=\dfrac{\dfrac{6-5}{

8}}{\dfrac{5-4}{8}}=\dfrac{{}^{1}/{}_{8}}{{}^{1}/{}_{8}}=\dfrac{1}{1}\].

Thus we can say that,

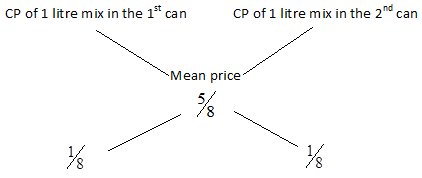
Thus ratio of the 2 mixtures = 1:1

So, quantity of mixture taken from each can = \[{}^{1}/{}_{2}\] litres of milk =
\[{}^{1}/{}_{2}\times 12=6\] litres of milk.

Thus mix 6 litres of water and 6 litres of milk to get the required mixture.
Note:Keep in mind the important points while applying the alligation method. While comparing the extreme values and mean price, you have to take the ‘difference’ between the two values, i.e. it is always positive, you have to subtract the smaller value from the larger value.