Question

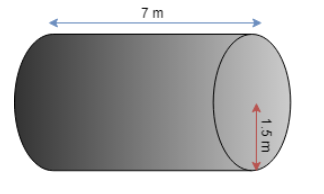
A milk tank is in the form of a cylinder whose radius is 1.5 m and length is 7 m. find the quantity of milk in litters that can be stored in the tank?

Answer 1

Hint: Use the fact the amount of milk that can be stored in cylinder will be equals to its volume thus, calculate the volume of the cylinder using the formula $\pi {r^2}h$

Complete step-by-step answer:
According to the given information we have a milk tank with radius 1.5 m i.e. r = 1.5 m and length of 7 m i.e. L = 7 m

We know that to find the capacity of milk tank we have to find the volume of the milk tank and the formula for the volume of the cylinder is given by $\pi {r^2}h$
Substituting the values in the above formula we get
Volume of milk tank =$\dfrac{{22}}{7} \times {\left( {1.5} \right)^2} \times \left( 7 \right)$
$ \Rightarrow $ Volume of milk tank = $\dfrac{{22}}{7} \times 2.25 \times 7$
$ \Rightarrow $ Volume of milk tank = $22 \times 2.25$
$ \Rightarrow $ Volume of milk tank = 49.5 ${m^3}$
Also, we know that $1{m^3} = 1000liters$
So, the capacity of milk tank to store milk = $49.5 \times 1000$
Capacity of milk tank to store milk = 49500 liters
Therefore, the milk tank can store 49500 liters milk


Note: In the above solution we found the capacity of the cylindrical shaped milk tank so the concept of cylinder can be explained as a three-dimensional shape which consist of 2 circular shaped bases which are parallel to each other also both the circular bases are connected with a curved surface here in the cylinder the perpendicular distance between the parallel circular shaped bases is named as the height of the cylinder.