Question

A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. If the approximate cost of milk at the rate of Rs. 22 per liter which the container can hold is Rs.________.

Answer 1

Hint: To solve this question we should know that the volume of the frustum is calculated using the formula \[\dfrac{1}{3}\pi h\left( r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right)\] where h is the height of the frustum, \[{{r}_{1}}\] and \[{{r}_{2}}\] are the radii of the upper and lower ends of the frustum. Also, we should know that 1 liter \[=1000c{{m}^{3}}\].

Complete step-by-step answer:
In this question, we have to find the cost of the milk at the rate of Rs. 22 per liter which the container can hold. Now, we will first find the volume of the container, so that we will be able to calculate the volume of the milk that a container can hold. Now, we know that the volume of the frustum is calculated using the formula \[\dfrac{1}{3}\pi h\left( r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right)\] where h is the height of the frustum, \[{{r}_{1}}\] and \[{{r}_{2}}\] are the radii of the upper and lower ends of the frustum.

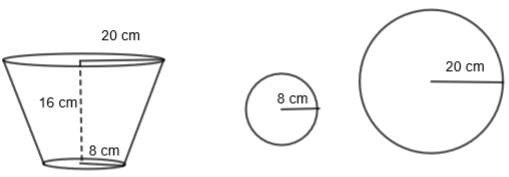
In the question, we have been given that the height of the container is 16 cm and radii of its lower and upper ends are 8 cm and 20 cm respectively. So, we can say h = 16 cm, \[{{r}_{1}}=8cm\] and \[{{r}_{2}}=20cm\]. Therefore, we will get the volume of the frustum as
\[Volume=\dfrac{1}{3}\times \pi \times 16\left[ {{\left( 8 \right)}^{2}}+{{\left( 20 \right)}^{2}}+8\times 20 \right]\]
Now, we will put \[\pi =\dfrac{22}{7}\] , and then we will simplify it. So, we will get,
\[Volume=\dfrac{1}{3}\times \dfrac{22}{7}\times 16\left[ 64+400+160 \right]\]
\[Volume=\dfrac{1}{3}\times \dfrac{22}{7}\times 16\times 624\]
\[Volume=\dfrac{73216}{7}\]
\[Volume=10459.42\text{ }c{{m}^{3}}\]
Now, we know that 1 liter \[=1000c{{m}^{3}}\] or we can say \[\dfrac{1}{1000}litre=1\text{ }c{{m}^{3}}\]. Therefore, we can write the volume in liters as,
Volume (in liters) \[=\dfrac{10459.42}{1000}liters\]
Volume (in liters) = 10.45942 liters
Now, we have to find the cost of the milk the container can hold. And the container can hold milk of volume as of volume of the container. So, the container can hold 10.45942 liters of milk.
Now, we have been given that the cost of 1 liter of milk is Rs. 22. Therefore, the cost of the milk in the container is
Cost of 10.45942 liters milk = (Volume of milk) \[\times 22\]
Cost of 10.45942 liters milk = \[10.45942\times 22\]
Cost of 10.45942 liters milk = Rs. 230.1024
Therefore, the approximate cost of milk is Rs. 230.10.

Note: This question contains a lot of calculation, so students have to be focused and be careful while doing the calculation. Also, remember that the volume of the frustum is calculated using the formula \[\dfrac{1}{3}\pi h\left( r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right)\] where h is the height of the frustum, \[{{r}_{1}}\] and \[{{r}_{2}}\] are the radii of the upper and lower ends of the frustum.