Question

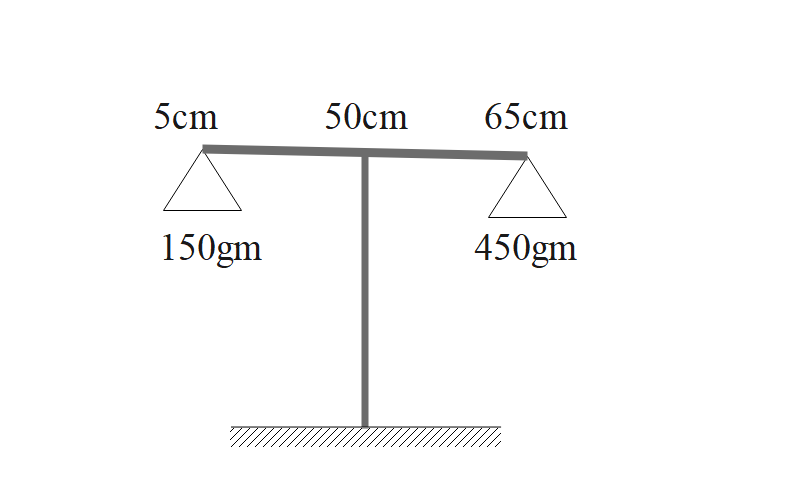
A metre scale is suspended at $50cm$ mark to a rigid support with a weight of $150gm$ attached at $5cm$ mark. To balance the scale, a weight of $450gm$ should be attached at _____cm mark.
$\begin{align}
 & a)65 \\
 & b)90 \\
 & c)95 \\
 & d)100 \\
\end{align}$

Answer 1

Hint: From the centre of the meter scale, the net moments on the left-hand side and the right-hand side must be equal. If we assume the weight is placed at some unknown distance to balance the net moment on the other side of the centre, on equalizing both the moments, we can find the distance at which the weight is placed to be balanced.

Formula used:
${{(weight\times length)}_{l}}={{(weight\times length)}_{r}}$

Complete answer:
Let us assume the weight is placed at a distance of x cm from the 50cm mark given.
For the meter scale to be balanced horizontally, moments on the left-hand side and the right-hand side must be balanced at the centre point.
I.e.,
Left hand moment=right hand moment,
$\begin{align}
  & 150\times 45=450\times x \\
 & \Rightarrow x=15cm....(1) \\
\end{align}$
Therefore, the weight must be placed at a distancer of $15cm$from the centre.
Now, to calculate the net distance of weight to be placed will be,
 $50+x.....(2)$
substitute equation (1) in equation(2),
$\Rightarrow 65cm$

So, the correct answer is “Option A”.

Additional Information:
Meter scale is the unit of measurement in the metric system. In this scale, ten centimetres is equal to one decimetre, ten decimetres are equal to one meter and thousand meters is equal to one kilometre. Balance scale is used to measure both mass and the distance at which the masses are suspended. Balance is used to measure the weights and the scale is used to measure the distance at which the weights are suspended. In modern weighing instruments, balances usually use a force restoration mechanism that creates a force to balance the force exerted by the unknown mass.

Note:
The distance that we get by equalizing the moments is the distance with respect to the meter scale. Usually, to find out the total distance at which the weight is placed, we need to add the position of meter scale on the big scale and the distance that we get with respect to centre of meter scale.