Question

A metallic sphere of radius 4.2cm is melted and recast into the shape of a cylinder of radius 6cm. Find the height of the cylinder.

Answer 1

Hint: The metallic sphere of radius 4.2cm is melted and recast into a cylinder with radius 6cm and height ‘h’. The volume of the sphere will be equal to the volume of the cylinder. Find the volume of sphere and cylinder. Equate it and find the height of the cylinder.

Complete step-by-step answer:
It is said that a metallic sphere of radius 4.2cm is melted into a cylinder of radius 6cm and height ‘h’.
 

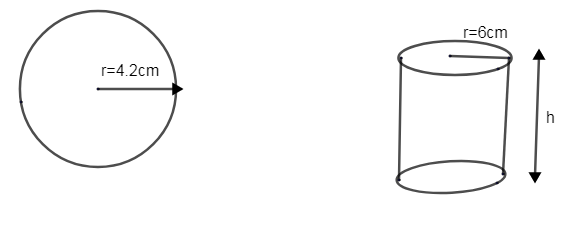
As the metallic sphere is melted and molded to a cylinder, their volume would be the same irrespective of their radius.
\[\therefore \]Volume of sphere = volume of cylinder.
Now let us find the volume of the sphere.
We know the radius, r of the given sphere = 4.2 cm
Volume of the sphere is given by\[\dfrac{4}{3}\pi {{r}^{3}}\].
\[\therefore \]Volume of sphere =\[\dfrac{4}{3}\pi \times {{\left( 4.2 \right)}^{3}}\].
Similarly, volume of cylinder with radius, r = 6cm and height ‘h’ cm is,
Volume of cylinder \[=\pi {{r}^{2}}h\]\[=\pi \times {{6}^{2}}\times h=36\pi h\]
Now, volume of sphere = volume of cylinder.
\[\dfrac{4}{3}\pi \times {{\left( 4.2 \right)}^{3}}=36\pi h\].
We need to find the height of the cylinder ‘h’.
\[\Rightarrow h=\dfrac{4\pi \times {{\left( 4.2 \right)}^{3}}}{3\times 36\pi }\]
Cancel out the like terms,
\[h=\dfrac{4\pi \times {{\left( 4.2 \right)}^{3}}}{3\times 36\pi }=\dfrac{4.2\times 4.2\times 4.2}{3\times 9}\]
                               \[\begin{align}
  & =\dfrac{4.2\times 4.2\times 4.2}{3\times 3\times 3}=1.4\times 1.4\times 1.4=2.744 \\
 & \therefore h=2.744cm \\
\end{align}\]
Hence, we found the height of the cylinder as 2.744cm.

Note: You should remember in questions like there that the volume would be the same irrespective of the radius given. As the sphere is melted down and recast to the cylinder, you should be able guess that the volume would remain the same, as the same quantity of melted sphere is used to recast the cylinder.