Question

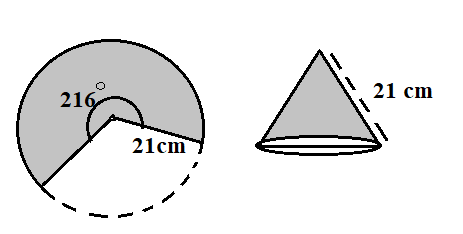
A metallic sheet in the form of a sector of a circle of radius 21 cm has central angle ${216^ \circ }$. The sector is made into a cone by bringing the bounding radii together. Find the volume of the cone formed.

Answer 1

Hint: We will first calculate the circumference of the sector which will be equal to the circumference of base of cone, use this equation to find the radius of the cone. Also, the radius of the semicircle will be the slant height of the cone. We will then find the perpendicular height using the formula, ${l^2} = {h^2} + {R^2}$, where $l$ is the slant height of the cone, $h$ is the perpendicular height and $R$ is the radius of the cone. Then, find the volume of the cone using the formula, $\dfrac{1}{3}\pi {R^2}h$.

Complete step-by-step answer:
We are given that the metallic sheet in the form of a sector has a radius of 21 cm and the central angle is ${216^ \circ }$.
The radius of the sector will act as the slant height of the cone.
Also, the circumference of the sector will be equal to the circumference of the base of the cone formed.

It is known that the circumference of the sector is $2\pi r\left( {\dfrac{\theta }{{360}}} \right)$, where \[r\] is the radius of the sector and $\theta $ is the central angle of the sector.
Therefore, we will substitute the given values in the above formula,
$2\left( {\dfrac{{22}}{7}} \right)\left( {21} \right)\left( {\dfrac{{216}}{{360}}} \right) = 79.2cm$
Let the radius of the base of the cone formed be $R$
Then, the circumference of the base of the cone is 79.2cm
$
  2\pi R = 79.2 \\
   \Rightarrow 2\left( {\dfrac{{22}}{7}} \right)R = 79.2 \\
   \Rightarrow R = \dfrac{{79.2\left( 7 \right)}}{{2\left( {22} \right)}} \\
   \Rightarrow R = 12.6cm \\
$
In a cone, ${l^2} = {h^2} + {R^2}$, where $l$ is the slant height of the cone, $h$ is the perpendicular height and $R$ is the radius of the cone.
We will now substitute the value of \[l\] and $R$ to find the value of $h$
$
  {\left( {21} \right)^2} = {h^2} + {\left( {12.6} \right)^2} \\
   \Rightarrow {h^2} = 441 - 158.76 \\
   \Rightarrow {h^2} = 282.24 \\
   \Rightarrow h = 16.8cm \\
$
Also, the volume of the cone is $\dfrac{1}{3}\pi {R^2}h$
Then, $V = \dfrac{1}{3}\left( {\dfrac{{22}}{7}} \right)\left( {12.6} \right)\left( {12.6} \right)\left( {16.8} \right) = 2794.176c{m^3}$
Hence, the volume of the cone formed is $2794.176c{m^3}$.

Note: The length of the boundary of the semicircle excluding its diameter will be equal to the length of the boundary of the base of the cone. One makes mistakes by taking the radius of the semicircle as perpendicular height of the cone, instead it is the slant height of the cone.