Question

A metallic right circular cone of 20 cm height whose vertical angle is $60^\circ $ is cut in two parts at needed of its height by a plane parallel to its base. If frustum so obtained be drawn into a wire of diameter $\dfrac{1}{{15}}$cm, find length of wire.

Answer 1

Hint:Here in the above question we are talking about the right circular cone.
First we will make frustum from the above given information.
We will cut the cone parallel to base.
Then by using trigonometric ratios we will find some dimensions and then final calculation for that we will equate both the volumes as wire is made from frustum.
We will take wire as a cylindrical figure. With its length as the height of the cylinder.
Formula used
Volume of cone $ = \dfrac{{\pi {r^2}H}}{3}$
Volume of frustum $ = \dfrac{{\pi h}}{3}(r_1^2 + r_2^2 + {r_1}{r_2})$
Volume of cylinder $ = \pi {r^2}H'$


Complete step by step solution :
Let OCD be the given cone, and ABCD to the required frustum.

.

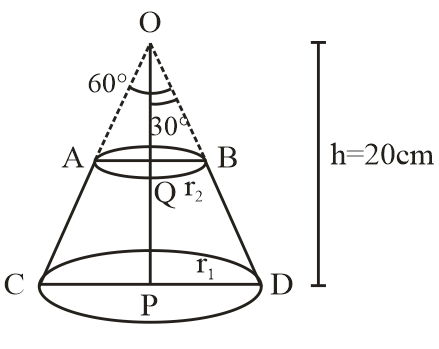
According to the question height $h(OP)$ is divided in 2 equal parts.
So, $OQ = OP = 10cm$
Here QP is also height of frustum
Let QB be the radius ${r_2}$ of frustum and PD, radius ${r_1}$ of frustum.
It is given that $\angle AOB = 60^\circ $
So, $\angle QOB = 30^\circ $
Now, we need to find ${r_1}$ and ${r_2}$.
In right $\Delta OPD$
$\tan \theta = \dfrac{{PD}}{{OP}}$
$\tan \theta = \dfrac{{{r_1}}}{{20}}$
$\tan 30^\circ = \dfrac{{{r_1}}}{{20}}$
${r_1} = \dfrac{{20}}{{\sqrt 3 }}cm$ …..(1)
In right triangle, $\Delta OQB$
$\tan \theta = \dfrac{{QB}}{{OQ}}$
$\tan 30^\circ = \dfrac{{{r_2}}}{{10}}$
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{{r_2}}}{{10}}$ or ${r_2} = \dfrac{{10}}{{\sqrt 3 }}cm$ …..(2)
Now, volume of frustum ABCD,

,

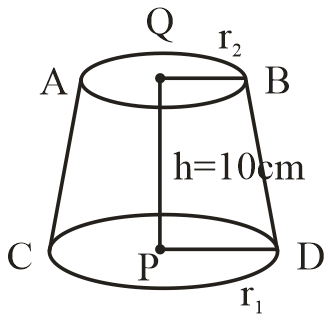
$Vf = \dfrac{{\pi h}}{3}(r_1^2 + r_2^2 + {r_1}{r_2})$
$ = \dfrac{{\pi \times 10}}{3}\left[ {{{\left( {\dfrac{{20}}{{\sqrt 3 }}} \right)}^2} + {{\left( {\dfrac{{10}}{{\sqrt 3 }}} \right)}^2} + \dfrac{{20}}{{\sqrt 3 }} + \dfrac{{10}}{{\sqrt 3 }}} \right]$
$Vf = \dfrac{{\pi 10}}{3}\left[ {\dfrac{{400}}{3} + \dfrac{{100}}{3} + \dfrac{{200}}{3}} \right]$
$Vf = \dfrac{{10\pi }}{{3 \times 3}}(700)$
$Vf = \dfrac{{700\pi }}{9}c{m^3}$ …..(3)
Now, volume of cylindrical were $ = \pi {r^2}h$
It is given that diameter of wire is $\dfrac{1}{{16}}cm$
So, radius $r = \dfrac{d}{2} = \dfrac{1}{{16 \times 2}} = \dfrac{1}{{32}}cm$

$r = \dfrac{1}{{32}}cm$
As length of wire is height of cylinder $ = $ h cm
Volume of wire $ = \pi {r^2}h$
$Vw = \pi {\left[ {\dfrac{1}{{32}}} \right]^2} \times h$ …..(4)
As wire is made of material used in frustum,
So volume of wire $ = $ volume of frustum
Therefore by equation 3 and 4
$Vw = Vf$
$\pi \times \dfrac{1}{{32 \times 32}} \times h = \dfrac{{700\pi }}{9}$
or, $h = \dfrac{{700 \times 32 \times 32}}{9}cm$
$h = \dfrac{{7168000}}{9} = 796444.4cm$
Therefore length of wire $ = 796444.4cm$
$ = 7964.4m$


Note : Here in calculation for radii ${r_1}$ and ${r_2}$ of frustum, we took two triangles.
Here is the explanation of finding $\tan \theta $.
Our diagram was

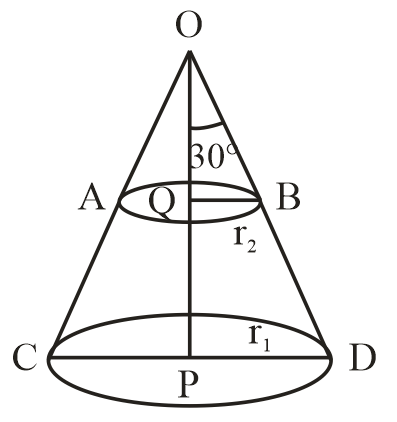
For $\Delta OQB$
$\angle Q = 90^\circ $ and $\theta $ is given at $\angle QOB$. So side opposite to $90^\circ $ i.e., OB $ = $ hypotenuse and side opposite to $\theta $ i.e., $\angle QOB$ is QB will be the perpendicular of $\Delta OQB$.
So, base $ = OQ = 10cm,$Hypotenuse $ = $ OB ; perpendicular $ = QB = $
We know that $\tan \theta = \dfrac{{perpendicular}}{{base}}$
$\tan \theta = \dfrac{{{r_2}}}{{10}}$
$\theta = 30^\circ $
$\tan 30^\circ = \dfrac{{{r_2}}}{{10}}$
So, ${r_2} = \dfrac{{10}}{{\sqrt 3 }}cm$
Same goes for triangle OPD.