Question

A metallic right circular cone 20cm high and whose vertical angle is \[60^\circ \] is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 1/16cm, find the length of the wire. ( Use \[\pi = \dfrac{{22}}{7}\] )

Answer 1

Hint:- Whenever any regular polygon is cut from the middle it will divide the figure into two equal parts and the common angles of the figure can also be divided into equal parts. Volume of frustum \[\dfrac{1}{3}\pi \times h({r_1}^2 + {r_2}^2 + {r_1} \times {r_2})\] will help us to find the length of wire because here the frustum is changed into wire.

Complete step-by-step answer:

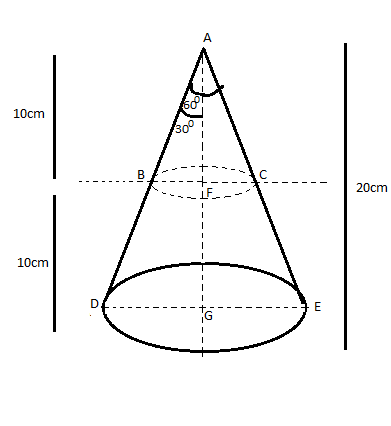
Now we had to solve the question according to this diagram.
As we know that when we cut the cone in two equal parts then the common angles will also get half so now the vertical angle which is \[60^\circ \] will now become \[30^\circ \] .
Now let us assume the upper radius of frustum as \[{r_1}\] and lower radius of frustum as \[{r_2}\].

Now in \[\vartriangle AFB\]
\[ \Rightarrow \]\[\tan 30^\circ = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}} = \dfrac{{FB}}{{AF}}\]
As the cone is cut from middle also to the height which is 20cm will now become 10cm and as we know that \[\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}\] so now putting these values in above equation.
\[ \Rightarrow \]\[\dfrac{1}{{\sqrt 3 }} = \dfrac{{FB}}{{10}} \Rightarrow FB = \dfrac{{10}}{{\sqrt 3 }}cm = {r_1}\]
Similarly, in \[\vartriangle AGD\]
\[ \Rightarrow \]\[\tan 30^\circ = \dfrac{{GD}}{{AG}} \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{GD}}{{20}}\]
\[ \Rightarrow \]\[GD = \dfrac{{20}}{{\sqrt 3 }}cm = {r_2}\]
Now as we know that volume of frustum must be equal to the volume of wire because wire is drawn out of frustum. And the volume of wire must be the area of cross – section per time length.
So volume of wire = \[\pi {r^2} \times {\text{length of wire}}\]
And diameter of wire = \[\dfrac{1}{{16}}cm\] so radius must be \[\dfrac{1}{{16}} \times \dfrac{1}{2} = \dfrac{1}{{32}}cm\]
And now volume of frustum = \[\dfrac{1}{3}\pi \times h({r_1}^2 + {r_2}^2 + {r_1} \times {r_2})\]
So now as volume of frustum = volume of wire
\[ \Rightarrow \] \[\dfrac{1}{3}\pi \times h({r_1}^2 + {r_2}^2 + {r_1} \times {r_2})\] = \[\pi {r^2} \times {\text{length of wire}}\]
Now putting all the values of \[{{\pi, }} {\text{h}}{{\text{,r}}_{\text{1}}}{\text{, }}{{\text{r}}_{\text{2}}}{\text{, r}}\]in above equation
\[ \Rightarrow \] \[\dfrac{1}{3} \times \dfrac{{22}}{7} \times 10 \times \left[ {{{\left( {\dfrac{{10}}{{\sqrt 3 }}} \right)}^2} + {{\left( {\dfrac{{20}}{{\sqrt 3 }}} \right)}^2} + \left( {\dfrac{{10}}{{\sqrt 3 }} \times \dfrac{{20}}{{\sqrt 3 }}} \right)} \right]{\text{ = }}\dfrac{{22}}{7} \times {\left( {\dfrac{1}{{32}}} \right)^2} \times l\]
Now we had to solve L.H.S and R.H.S to get the value of length of wire ( l ).
\[ \Rightarrow \] \[\dfrac{1}{3} \times 10 \times \left[ {\left( {\dfrac{{100}}{3}} \right) + \left( {\dfrac{{400}}{3}} \right) + \left( {\dfrac{{200}}{3}} \right)} \right]{\text{ }} = {\text{ }}\left( {\dfrac{1}{{1024}}} \right) \times l\]
\[ \Rightarrow \] \[\dfrac{{10}}{3} \times \dfrac{{700}}{3}{\text{ }} = {\text{ }}\dfrac{1}{{1024}} \times l\]
\[ \Rightarrow \] \[\dfrac{{7000}}{9} \times 1024{\text{ }} = {\text{ }}l\]
So, the length of wire ( l ) = 796444.44 cm.

Note :- Whenever we come up with this type of problem in which a shape is converted or changed into the other we had to know that in such cases the total area of both the shapes may be differ from each other even though the material and the amount is same but the volume of both the shapes must be equal to each other. We can also solve this question by finding one of the volumes ( either of frustum or of wire ) and then keeping each other equal . in that case the calculation will be a little more because at that time we had to solve the value of \[\pi = \dfrac{{22}}{7}\] as well but here we don’t have to solve this because both the \[\pi \] of L.H.S and R.H.S will cancel each other.