Question

A metallic pipe 0.7 cm thick. Inner radius of the pipe is 3.5 cm and length is 5 dm. Find its total surface area.

Answer 1

Hint: The total surface area of a cylindrical pipe is equal to the sum of inner curved surface area, outer curved surface area and the area of the rims at both the ends of the pipe. Don’t forget to convert all the quantities to proper units before using them in the formulas.

Complete step-by-step answer:
To start with the question let us draw the diagram of the pipe.

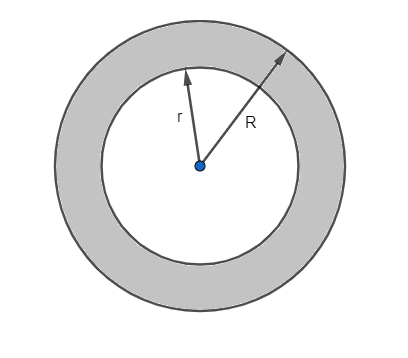
The above diagram shows the view of the pipe if we see it from one end.
Now first let us find the inner curved surface area of the cylindrical pipe. It is given that the inner radius r of the pipe is 3.5 cm and length of the cylinder is 5 dm, which is equal to 50 cm.
$\text{Inner curved surface area =2}\pi rh$ .
Also, the outer curved surface area of the cylindrical pipe can be found using the outer radius, which is equal to r + thickness = 3.5+07=4.2 cm. Height in this case also remains the same.
$\text{Outer curved surface area =2}\pi {{R}}h=2\pi \left( r+0.7 \right)h$
We can also see from the figure that the area of the rim on one side is equal to the area of the larger circle minus the area of the smaller circle, and there are 2 such rims, one at each end.
$\text{Area of the 2 rims =2}\left( \pi {{R}^{2}}-\pi {{r}^{2}} \right)=2\left( \pi {{\left( r+0.7 \right)}^{2}}-\pi {{r}^{2}} \right)$
Now the total surface area of a cylindrical pipe is equal to the sum of inner curved surface area, outer curved surface area and the area of the rims at both the ends of the pipe.
$\therefore \text{Total surface area=2}\pi rh+2\pi \left( r+0.7 \right)h-2\pi {{r}^{2}}+2\pi {{\left( r+0.7 \right)}^{2}}$
$\Rightarrow \text{Total surface area=}\left( 3.5\times 50+\left( 3.5+0.7 \right)\times 50-{{\left( 3.5 \right)}^{2}}+{{\left( 3.5+0.7 \right)}^{2}} \right)2\pi $
$\Rightarrow \text{Total surface area=}\left( 175+210-12.25+17.64 \right)2\pi $
\[\Rightarrow \text{Total surface area=780}\text{.78}\pi \]
Now if we put the value of $\pi =3.14$ , we get
\[\text{Total surface area=2451}\text{.65c}{{\text{m}}^{2}}\]
Therefore, the answer to the above question is 2451.65 sq. cm.

Note: The first thing to keep in mind in such questions is that the area of the rim must be considered and cannot be neglected. Also, be careful about the calculation part as there is a high chance of making a mistake in the calculation part.