Question

A metallic chain 1m long lies on a horizontal surface of a table. The chain starts sliding on the table if $25cm$ (or more of it) hangs over the edge of a table. The correct value of the coefficient of friction between the table and the chain is
\[(A)\dfrac{1}{3}\]
\[(B)\dfrac{2}{3}\]
\[(C)\dfrac{1}{4}\]
\[(D)\dfrac{1}{5}\]

Answer 1

Hint: In order to find the correct value of the coefficient of friction between the table and the chain, we need to equate the forces which are acting on the metallic chain. The force is the force of gravity which is acting on the part of the chain which is hanging. The other force is the force of friction and this acts on the part of the chain which is lying on the table. On equating these two forces, we will get the answer.

Complete step by step solution:
The diagram for the given question is:

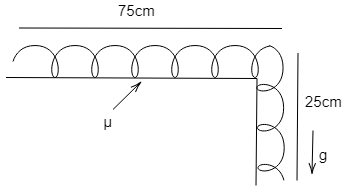
According to the question,
Let us consider the mass of this particular chain be $m$
In the question, it is given that the chain starts sliding on the table if $25cm$ (or more of it) hangs over the edge of a table. The chain starts moving, which means that the force of gravity becomes equal to the force of friction.
So, we can write that,
Force of gravity on $25cm$ of chain = Force of friction on the rest $75cm$ of chain (equation 1)
Force of gravity on $25cm$ of chain $ = 0.25mg$
Similarly, Force of friction on the rest $75cm$ of chain $ = 0.75\mu mg$
On putting the value of the above two forces in equation 1, we get,
$0.25mg = 0.75\mu mg$
On cancelling the common terms on both the sides,
$0.25 = 0.75\mu $
$\mu = \dfrac{{0.25}}{{0.75}}$
On simplifying the fraction,
$\mu = \dfrac{1}{3}$
The correct value of the coefficient of friction between the table and the chain is $\mu = \dfrac{1}{3}$.
So, the final answer is \[(A)\dfrac{1}{3}\].

Note:
It is important to note that there are basically two types of forces of friction. The first force of friction is the static force of friction and this force of friction acts on a body when the body is in a state of rest. The other type of force of friction is the kinetic force of friction and this force of friction acts on a body which is in motion.