Question

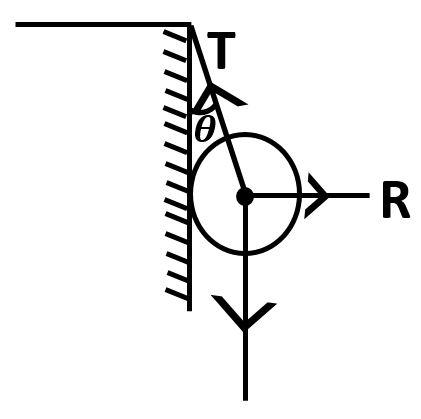
A metal sphere is hung by a string fixed to a wall. The forces acting on the sphere are shown in figure. Which of the following statements are true:
(a) $\overrightarrow R + \overrightarrow T + \overrightarrow W = 0$
(b) ${T^2} = {R^2} + {W^2}$
(c) $T = R + W$
(d) $R = W\tan \theta $

A. $a,b,c$
B. $b,c,d$
C. $a,b,d$
D. $a,b,c,d$

Answer 1

Hint: Draw a free body diagram of the given figure then use the condition of equilibrium to solve the questions.

Complete step by step answer:
Observe the diagram

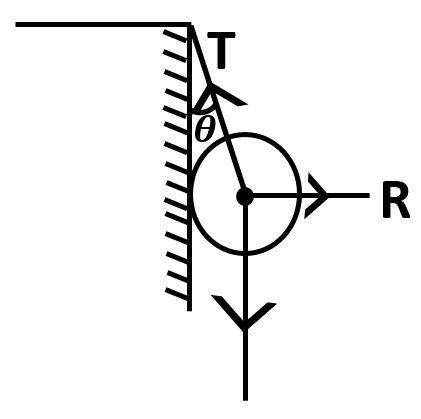
We will now draw the free body diagram of the above figure.
Where,
$R$ is the reaction force acting on the sphere due to the wall.
$T$ is the tension in the string
$W = mg$ is the weight of the sphere.
Now, the sphere is not moving. That means, the sphere is in the equilibrium position.
We know that,
In equilibrium position, the vector sum of all the forces acting on the body is equal to zero.
$\therefore \vec R + \vec T + \vec W = 0$
Hence, (a) is correct
We can resolve the components of tension on the string as shown in the figure.
Observing the figure, you can see that $T\cos \theta $ and $W$ are acting exactly opposite to each other.
And since there is no movement in the sphere. We can say that these two forces must be equal in magnitude to balance each other.
$ \Rightarrow T\cos \theta = W$
In the same way, you can observe that the reaction force $R$ and the component of tension $T\sin \theta $are exactly opposite to each other. So, again since the sphere is in equilibrium position the two forces must be equal in magnitude to balance each other.
$ \Rightarrow T\sin \theta = R.........(2)$
By dividing equation (2) by equation (1) we get
$\dfrac{{T\sin \theta }}{{T\cos \theta }} = \dfrac{R}{W}$
$ \Rightarrow \tan \theta = \dfrac{R}{W}$
By cross multiplying and rearranging we get.
$R = w\tan \theta $
Therefore, Option (d) is correct.
Now, by squaring equation (1) and (2) and then adding them to each other we get.
\[{T^2}{\cos ^2}\theta + {T^2}{\sin ^2}\theta = {W^2} + {R^2}\]
\[ \Rightarrow {T^2}({\cos ^2}\theta + {\sin ^2}\theta ) = {W^2} + {R^2}\]
But \[{\cos ^2}\theta + {\sin ^2}\theta = 1,\]Therefore we can write.
${T^2} = {W^2} + {R^2}$
Therefore, Option (b) is correct.
Clearly, $T \ne R + W$ $(\because {T^2} = {R^2} + {w^2})$
Thus, option a, b and d are correct
Therefore, from the above explanation, the correct answer is, option (C) a, b, d

Note:To solve this question you need to know how to draw a free body diagram. It is important to know what the state of equilibrium is. And that the vector sum of all the force acting on the body in equilibrium is equal to zero. That also means that the vector sum of all the forces acting along the X-axis is equal to zero and the vector sum of all the forces acting along the y-axis is equal to zero.