Question

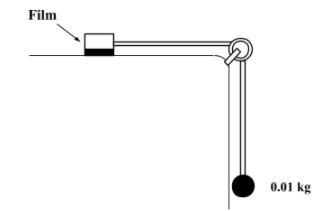
A metal block of area $0.10 {m}^{2}$ is connected to a 0.01 kg mass via a string that passes over a massless and frictionless 0.01 kg pulley as shown in figure. A liquid with a film thickness of 0.3 mm is placed between the block and the table. When released the block moves to the right with a constant speed of $0.085 m{s}^{-1}$. The coefficient of viscosity of the liquid is (Take g = $10 m{s}^{-2}$)
A. $2.5 \times {10}^{-3} Pa s$
B. $3.5 \times {10}^{-3} Pa s$
C. $4.5 \times {10}^{-3} Pa s$
D. $6.5 \times {10}^{-3} Pa s$

Answer 1

Hint: Use the formula for coefficient of viscosity of liquid to solve this problem. Coefficient of viscosity is the ratio of shear stress to strain rate. But, both these parameters are not given. Thus, using the formula for shear stress calculate the value of shear stress. Then, using the formula for strain rate, calculate it’s value. Substitute these obtained values in the formula for coefficient of viscosity and thus, you will get the coefficient of viscosity of liquid.

Complete step by step answer:
Given: Area (A) =$0.10 {m}^{2}$
Mass (m)= 0.01 kg
Thickness (t)= 0.3 mm
$g$ = $10 m{s}^{-2}$
Speed ($v$)= $0.085 m{s}^{-1}$
The formula for coefficient of viscosity is given by,
$\eta = \dfrac {Shear\,\, stress}{Strain\,\,rate}$ ...(1)
Shear stress is given by,
$Shear \, \, stress = \dfrac {Shear \,\, force}{Area}$ ...(2)
But, Shear force is given by,
$F= mg$
Substituting values in above equation we get,
$\Rightarrow F= 0.01 \times 10$
$\therefore F= 0.1 N$
Thus, substituting values in equation (2) we get,
$\Rightarrow Shear \, \, stress = \dfrac {0.1}{0.10}$
$\therefore Shear \, \, stress= 1 {N}{{m}^{-2}}$ ...(3)
Now, Strain rate is given by,
$Strain \,\, rate= \dfrac {speed}{thickness}$
Substituting values in above equation we get,
$\Rightarrow Strain \,\, rate= \dfrac {0.085}{0.3 \times {10}^{-3}}$
$\therefore Strain \,\, rate= 283.33 {s}^{-1}$ ...(4)
Now, substituting the equation. (3) and equation. (4) in equation. (1) we get,
$\Rightarrow \eta = \dfrac {1}{283.33}$
$\Rightarrow \eta = 0.0035 Pa s$
$\therefore \eta= 3.5 \times {10}^{-3} Pa s$
Thus, the coefficient of viscosity of liquid is $3.5 \times {10}^{-3} Pa s$.

Hence, the correct answer is option B i.e. $3.5 \times {10}^{-3} Pa s$.

Note:
To solve these kinds of problems, students should remember the formula for all the parameters. There are different viscosities like Dynamic viscosity and Kinematic viscosity. Dynamic viscosity tells us about the force required to make a fluid flow at a certain rate. While, the kinematic viscosity tells us at which rate the liquid will flow when a certain force is applied. The Units of both the viscosities are not the same.