Question

A matchbox measures $4cm\times 2.5cm\times 1.5cm$. What will be the volume of the packet containing 12 such boxes.

Answer 1

Hint: First, we should know the formula which we are going to use to calculate the volume of the matchbox which is actually a cuboid as $V=l\times b\times h$ . Then, we have to substitute the value of length, breadth and height in the formula of the volume of the cuboid and calculate the volume. Then, to get the volume of such 12 boxes, we multiply the calculated volume with 12 and get the volume of the 12 such boxes means that we have 12 cuboids of equal volume arranged in a packet which actually forms a large cuboid.

Complete step-by-step answer:
In this question, we are supposed to find the volume of the matchbox which is a cuboid of dimension $4cm\times 2.5cm\times 1.5cm$.

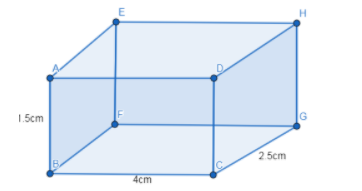
The volume V of the cuboid is given by the formula where $l$ is length, $b$ is breadth and $h$ is height as:
$V=l\times b\times h$
From the figure, we can find the length as $l=4cm$, breadth as $b=2.5cm$ and height as $h=1.5cm$.
Now, we will substitute the values of length, breadth and height in the above stated formula and calculate the volume of cuboid as asked in the question:
$\begin{align}
  & V=4cm\times 2.5cm\times 1.5cm \\
 & \Rightarrow V=15c{{m}^{3}} \\
\end{align}$
The above calculation gives us the volume of one matchbox as $15c{{m}^{3}}$.
Now, we need to find the volume of 12 such matchboxes in the question.
We know 12 such boxes means that we have 12 cuboids of equal volume arranged in a packet which actually forms a large cuboid.
So, to get the volume of 12 such boxes we multiply the calculated volume to 12.
$\begin{align}
  & 15c{{m}^{3}}\times 12 \\
 & \Rightarrow 180c{{m}^{3}} \\
\end{align}$
Hence, the volume of the packet containing 12 such boxes is $180c{{m}^{3}}$.


Note: The special thing about the volume of the cuboid is that while calculating the volume of the cuboid we can take any side as length, breadth or height for the reason that at the end, they are just going to be multiplied and we get the same answer in every condition. Now, to justify it we know that $1\times 2$ or $2\times 1$ both yields the same result. So, we can consider any side of the cuboid as length, breadth or height and calculate the volume of the same. We always get the correct answer.