Question

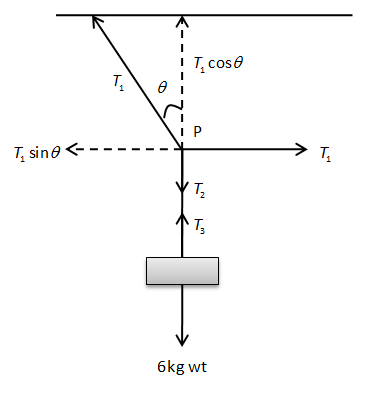
A mass of 6 kg is suspended by a rope of length 2 m from the ceiling. A force of 50 N in the horizontal direction is applied at the midpoint P of the rope. As shown. What is the angle the rope makes with the vertical in equilibrium? (take \[g = 10\,ms^{ - 2} \]). Neglect the mass of the rope.

Answer 1

Hint: Apply Newton’s second law of motion at point P and balance the forces.
In the given question, the mass is not moving vertically downwards. Therefore, the whole system is in the equilibrium. Thus, applying Newton’s second law at any point on the rope will give the tension force.

Complete step by step answer:
Let us apply Newton’s second law at point P in the horizontal direction.
\[
F_{horizontal} = ma
\]


Here, \[
F_{horizontal}
\] is the net horizontal force.

Therefore,
\[
T_1 - T_1 \sin \theta = ma
\]

Since mass is not moving, the acceleration of the mass is zero. Therefore, the above equation will become,
\[
T_1 - T_1 \sin \theta = m\left( 0 \right)
\]

\[
 \Rightarrow T_1 \sin \theta = T_1
\]
                                                                                                                                              ...... (1)

Let us apply Newton’s second law at point P in the vertical direction.
\[
F_{vertical} = ma
\]


Here, \[F_{vertical} \] is the net vertical force.

Therefore,
\[
T_1 \cos \theta - T_2 = ma
\]


Since mass is not moving, the acceleration of the mass is zero. Therefore, the above equation will become,\[T_1 \cos \theta - T_2 = m\left( 0 \right)\]

\[
 \Rightarrow T_1 \cos \theta = T_2
\]
                                                                                                                                             ...... (2)

Since the mass is in the equilibrium, the tension \[T_2 \] is balanced by the tension \[T_3 \]. Also, the tension in the rope \[T_3 \] must be equal to the weight of the mass.

The mass is 6 kg wt. Therefore, the weight of the mass is,
\[
W = mg
\]


Here, \[m\] is the mass and \[g\] is the acceleration due to gravity.

Therefore,
\[
W = \left( {6\,kg\,wt} \right)\left( {10\,ms^{ - 2} } \right)
\]

\[
W = 60\,N
\]


Therefore, \[
T_3 = W = 60\,N
\].

Substitute \[T_3 \] for \[T_2 \] in equation (2).
\[T_1 \cos \theta = T_3 \]

Divide equation (1) by the above equation, we get,
\[
\dfrac{{T_1 \sin \theta }}
{{T_1 \cos \theta }} = \dfrac{{T_1 }}
{{T_3 }}
\]

\[
\dfrac{{\sin \theta }}
{{\cos \theta }} = \dfrac{{T_1 }}
{{T_3 }}
\]

\[
 \Rightarrow \tan \theta = \dfrac{{T_1 }}
{{T_3 }}
\]


Substitute 50 N for \[T_1 \] and 60 N for \[T_3 \] in the above equation.
\[
\tan \theta = \dfrac{{50\,N}}
{{60\,N}}
\]

\[
\tan \theta = \dfrac{5}
{6}
\]

\[
 \Rightarrow \theta = \tan ^{ - 1} \left( {\dfrac{5}
{6}} \right)
\]

\[
\therefore \theta = 39.8^\circ
\]


Therefore, the makes an angle \[
39.8^\circ
\]
 with the vertical.

Note:
while applying Newton’s second law at a point be specific with the direction of forces. One can assume the force acting towards the right of the point P as a positive and towards the left as negative or vice versa. Also, assume the force acting upward as positive and the force acting downward as negative.