Question

A mass of $10kg$ is suspended by a rope of length $4m$ , from the ceiling. A force $F$ is applied horizontally at the midpoint of the rope such that the top half of the rope makes an angle ${45^ \circ }$ with the vertical. Then $F$ equals: (Take $g = 10m{s^{ - 2}}$ and the rope to be massless)
A. $70N$
B. $75N$
C. $100N$
D. $90N$

Answer 1

Hint: Initially the body was suspended vertically and the Tension force and gravitational pull of Earth was balanced. Later, a force was applied and it makes an angle ${45^ \circ }$ with the horizontal. Split the forces in components. And then balance the forces vertically as well as horizontally.

Complete step by step answer:
In these types of questions it is better to draw the diagram and then balance the forces. So, let us first draw the diagram when force $F$ is applied horizontally at the midpoint of the rope such that the top half of the rope makes an angle ${45^ \circ }$ with the vertical.

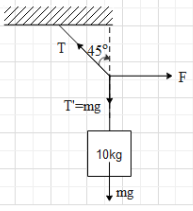
Please note that the red lines indicate the forces.Now we know that at this position, the body is in equilibrium so all the forces at this instant must be balanced. We have to split the force due tension in horizontal as well as vertical direction as given.Don’t forget that the gravitational pull is always acting on the body.

Horizontally there are two forces acting on the body, the force applied externally and the sine component of tension force. Since, the body is not performing any motion in horizontal direction, therefore the forces in horizontal direction must be balanced.
$T\sin {45^ \circ } = F$
(Here, T is the tension in the rope).
$ \Rightarrow \dfrac{T}{{\sqrt 2 }} = F$ --equation $1$
Also, vertically two forces are acting on the block. So, these two forces also must be balanced, as the body is not performing any motion in the vertical direction.
$T\cos {45^ \circ } = mg$
(Here, mg is the gravitational force acting on the body).
The mass of the body is given to be $10kg$ and the value of acceleration due to gravity is also given as $g = 10m{s^{ - 2}}$
$ \Rightarrow \dfrac{T}{{\sqrt 2 }} = 10 \times 10$
$ \Rightarrow T = \sqrt 2 \times 100$
Substituting this value in equation $1$ we have:
$\dfrac{T}{{\sqrt 2 }} = F$
$ \Rightarrow \dfrac{{\sqrt 2 \times 100}}{{\sqrt 2 }} = F$
$ \therefore F = 100N$
Therefore, the force $F$ equals $100N$ .

Hence, option C is the correct option.

Note: Diagrams are very helpful in these types of problems. Draw a free body diagram to get a better idea of the forces. The forces in all the directions must be balanced as the block is in stable condition. The direction of gravitational force will always be towards the ground.Note that in the given case, the tension in the two segments of the rope will be different because of the force F. The tension in the lower section of the rope is equal to the gravitational force, i.e. mg.