Question

A mass of $0.2kg$ is whirled in a horizontal circle of radius $0.5m$ by a string inclined at $30^\circ $ to the vertical. Calculate the tension in the string and the speed of the mass in the horizontal circle?

Answer 1

Hint:This question utilizes the concept of mechanics and free body diagrams. We need to draw the free body diagram of the mass which is whirled and then equate the forces acting on them in the vertical and horizontal direction.

Formulae used :
${F_c} = \dfrac{{m{v^2}}}{r}$ where ${F_c}$ is the centripetal force acting on the body, $m$ is the mass of the body and $v$ is the velocity of the body and $r$ is the radius of the circle.
Acceleration due to gravity $g = 9.8m{s^{ - 2}}$

Complete step by step answer:
Let the body which is whirled around be $A$ . Let it be spinning from a point $B$ with a rope with tension $T$ in it .
According to the question, it is inclined at $30^\circ $ to the vertical.
Then, the angle it will make with the horizontal will be
$
   \Rightarrow \theta = 90^\circ - 30^\circ \\
   \Rightarrow \theta = 60^\circ \\
 $
Mass of the body $A$ is $m = 0.2kg$
Radius of the circle which is made when $A$ is whirled $r = 0.5m$
Now, a free body diagram is made to understand better.

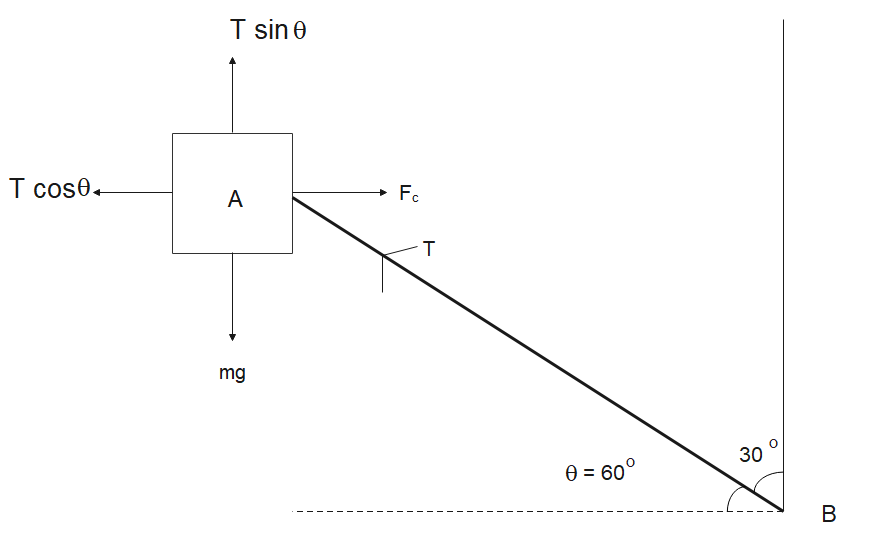
First, we balance out the vertical forces acting on $A$ .
We have a component of the tension of the string, which is pushing the body upwards. Then we have the weight of the body which is pulling it downwards.
Since the body is in equilibrium, these two forces must be equal to each other.
Thus, we have

$ \Rightarrow T\sin \theta = mg$
Putting in the respective values, we have
$
   \Rightarrow T\sin 60^\circ = 0.2kg \times 9.8m{s^{ - 2}} \\
   \Rightarrow T = \dfrac{{0.2 \times 9.8}}{{\sin 60^\circ }}N \\
   \Rightarrow T = \dfrac{{1.96}}{{0.866}}N \\
   \Rightarrow T = 2.26N \\
 $
Therefore, the tension on the string is $2.26N$
Now, while balancing out the horizontal forces, we see that the centripetal force is balanced out by the horizontal component of tension. Thus we have
$ \Rightarrow {F_c} = T\cos \theta $
$ \Rightarrow \dfrac{{m{v^2}}}{r} = T\cos \theta $
Putting in the respective values, we get
$
   \Rightarrow \dfrac{{0.2kg \times {v^2}}}{{0.5m}} = 2.26N \times \cos 60^\circ \\
   \Rightarrow {v^2} = \dfrac{{2.26 \times 0.5 \times 0.5}}{{0.2}}{\left( {m{s^{ - 1}}} \right)^2} \\
   \Rightarrow {v^2} = \left( {11.3 \times 0.5 \times 0.5} \right){\left( {m{s^{ - 1}}} \right)^2} \\
 $
Now, using square root on both the sides, we get
$
   \Rightarrow v = 3.36 \times 0.5m{s^{ - 1}} \\
   \Rightarrow v = 1.68m{s^{ - 1}} \\
 $
Therefore, the speed of the mass in the horizontal circle is $1.68m{s^{ - 1}}$.

Note: Students usually get confused when resolving a vector into two parts. Just remember that the vertical component of the vector is the vector multiplied by $\sin \theta $ and the horizontal component is the vector multiplied by $\cos \theta $ . Here, $\theta $ is the angle between the vector and the $x$ axis.