Question

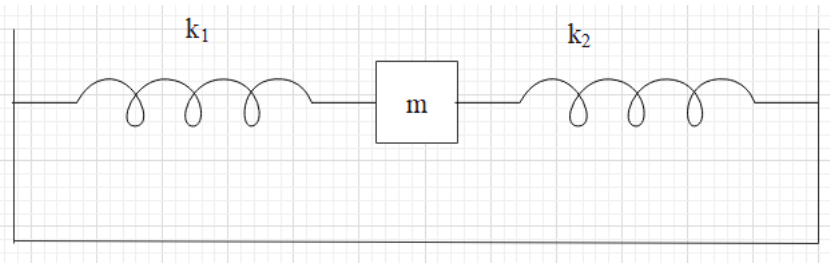
When a mass $m$ which is vibrating with spring of spring constant ${{k}_{1}}$​. Its frequency will be \[3Hz\] and with spring of spring constant \[{{k}_{2}}\] ​and its frequency will be \[6Hz\]. Then what will be the frequency of oscillations when mass is connected with spring as represented in the diagram?

\[\begin{align}
  & A.6.7 \\
 & B.4.5 \\
 & C.9 \\
 & D.3 \\
\end{align}\]

Answer 1

Hint: The frequency can be found by taking the square root of the ratio of the spring constant to the mass of the spring. Find out the equation for both the spring constant. As these two springs are parallel then their resultant spring constant will be found by taking the sum of both the spring constant. Calculate the resultant frequency also. This will help you in answering this question.

Complete answer:
The frequency can be found by taking the square root of the ratio of the spring constant to the mass of the spring. That is,
\[{{\omega }_{1}}=\sqrt{\dfrac{{{k}_{1}}}{m}}\]
As the frequency has been mentioned to be \[3Hz\], substituting this in the equation will give,
\[\begin{align}
  & 3=\sqrt{\dfrac{{{k}_{1}}}{m}} \\
 & \Rightarrow {{\left( 3 \right)}^{2}}m={{k}_{1}}=9m \\
\end{align}\]
In the same way, for the spring constant \[{{k}_{2}}\], we can write that,
\[{{\omega }_{2}}=\sqrt{\dfrac{{{k}_{2}}}{m}}\]
As the frequency for this case has been mentioned in the question as,
\[{{\omega }_{2}}=6Hz\]
Substituting this value in the equation will give,
\[\begin{align}
  & 6=\sqrt{\dfrac{{{k}_{2}}}{m}} \\
 & \Rightarrow {{\left( 6 \right)}^{2}}m={{k}_{2}} \\
 & \therefore 36m={{k}_{2}} \\
\end{align}\]
Now both the springs are connected in parallel. Therefore we can write that the resultant spring constant will be found by taking the sum of both the spring constant. That is,
\[{{k}_{net}}={{k}_{1}}+{{k}_{2}}\]
Substituting the values in it will give,
\[{{k}_{net}}=9m+36m=45m\]
Therefore the net frequency can be found by the equation,
\[{{\omega }_{net}}=\sqrt{\dfrac{{{k}_{net}}}{m}}\]
Substituting the values in it will give,
\[{{\omega }_{net}}=\sqrt{\dfrac{45m}{m}}=\sqrt{45}Hz=6.7Hz\]

Hence the correct answer has been obtained as option A.

Note:
The frequency of oscillation has been defined as the total number of complete oscillations a body is performing in a unit time period. It can be found by taking the reciprocal of the time period of the body. The unit can be expressed in hertz.