Question

A mass m moves with a velocity v and collides inelastically with another identical mass. After the collision, the first mass moves with velocity $\dfrac{v}{{\sqrt 3 }}$ in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after the collision
A. $\dfrac{{2v}}{{\sqrt 3 }}$
B. $\dfrac{v}{{\sqrt 3 }}$
C. $v\sqrt {\dfrac{2}{3}} $
D. The situation of the problem is not possible without external impulse

Answer 1

Hint:In extreme cases of inelastic collision, the masses stick together. In an inelastic collision, the kinetic energy is not conserved; only the total energy is conserved. Almost all macroscopic collisions are inelastic. Remember that after sticking together, the composite body moves with one velocity ${v_1}$, and the mass will be the sum of both ${m_1} + {m_2}$.

Complete step by step answer:
Refer to the below figure for a proper explanation. The velocities are shown before and after the collision. The upward Y direction's velocity is taken as positive and the velocities in the downward Y direction are taken as negative.

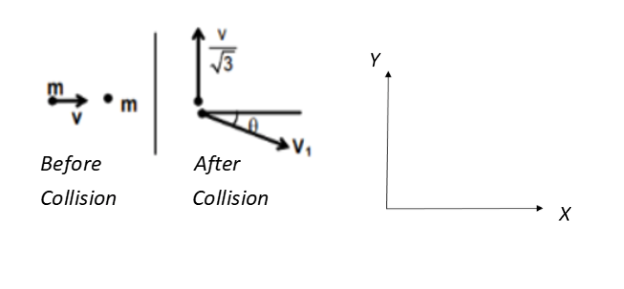
We know that the momentum is conserved to apply the conservation of momentum in the X-direction.
$\begin{array}{l}
mv = m{v_1}\cos \theta \\
v = {v_1}\cos \theta \;......\;\left( 1 \right)
\end{array}$
We will now apply the conservation of momentum in the Y direction.
$\begin{array}{l}
0 = \dfrac{{mv}}{{\sqrt 3 }} - m{v_1}\sin \theta \\
\dfrac{v}{{\sqrt 3 }} = {v_1}\sin \theta \;......\left( 2 \right)
\end{array}$
Now squaring and adding equation (1) and (2), we get,
\[\begin{array}{l}
{v^2} + \dfrac{{{v^2}}}{{{{\left( {\sqrt 3 } \right)}^2}}} = v_1^2{\cos ^2}\theta + v_1^2{\sin ^2}\theta \\
\dfrac{{4{v^2}}}{3} = v_1^2\left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right)
\end{array}\]
We know that $\left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right)$=1, therefore the above equation becomes,
\[\begin{array}{l}
\dfrac{{4{v^2}}}{3} = v_1^2\\
{v_1} = \dfrac{{2v}}{{\sqrt 3 }}
\end{array}\]

Therefore, the correct option is (A).

Additional Information:Normally, all common collisions are considered to be inelastic. For a collision to be considered elastic, it's kinetic energy and momentum/energy should be conserved. The kinetic energy is not conserved in ordinary collisions due to the action of internal friction. In most natural cases, some of the kinetic energy is converted to other forms. For example, in some cases, kinetic energy is converted into the atom's vibrational energy, in some others, as sound energy, etc.

Note:In the inelastic collision, the combined momentum of the two bodies continues the same, but some of the initial kinetic energy is changed into heat energy inside the bodies, which are used up in misshaping the bodies or discharged away in some other method.