
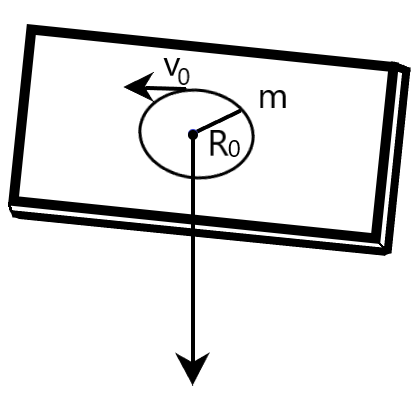
A mass $m$ moves in a circle on a smooth horizontal plane with velocity ${{v}_{0}}$, at a radius ${{R}_{0}}$. The mass is attached to a string which passes through a smooth hole in the plane as shown. The tension in the string is increased gradually and finally $m$ moves in a circle of radius $\dfrac{{{R}_{0}}}{2}$. The final value of kinetic energy is
$\begin{align}
& A)2m{{v}_{0}}^{2} \\
& B)\dfrac{1}{2}m{{v}_{0}}^{2} \\
& C)m{{v}_{0}}^{2} \\
& D)\dfrac{1}{4}m{{v}_{0}}^{2} \\
\end{align}$

Answer
571.5k+ views
Hint: Kinetic energy of a particle is proportional to the mass of particle as well as the square of velocity of particle. When a particle rotates about an axis, angular momentum of the particle is defined as the product of mass of particle, velocity of particle and the radius of the circular path, through which the particle rotates. It is a conserved quantity.
Formula used:
$\begin{align}
& 1)L=mvr \\
& 2)KE=\dfrac{1}{2}m{{v}^{2}} \\
\end{align}$
Complete step-by-step answer:
When a particle rotates about an axis, angular momentum of the particle is defined as the product of mass of particle, velocity of particle and the radius of the circular path, through which the particle rotates. It is a conserved quantity. Mathematically, angular momentum is given by
$L=mvr$
where
$L$ is the angular momentum of a rotating particle
$m$ is the mass of particle
$v$ is the velocity of particle
$r$ is the radius of circular path, through which the particle rotates
Let this be equation 1.
Coming to our question, we are given with a mass $m$, which moves in a circle on a smooth horizontal plane with velocity ${{v}_{0}}$, at a radius ${{R}_{0}}$. The mass is attached to a string which passes through a smooth hole in the plane as shown in the following figure. The tension in the string is increased gradually and finally, the mass $m$ moves in a circle of radius $\dfrac{{{R}_{0}}}{2}$. We are required to determine the final value of kinetic energy.
Let us assume the velocity of mass $m$, which when rotates in a circular path of radius $\dfrac{{{R}_{0}}}{2}$, to be $v'$.
Using equation 1, angular momentum of the mass before the application of tension is given by
$L=m{{v}_{0}}{{R}_{0}}$
where
$L$ is the angular momentum of mass
$m$ is the given mass
${{v}_{0}}$ is the velocity of mass, before the application of tension
${{R}_{0}}$ is the radius of circular path, through which the mass rotates before the application of tension
Let this be equation 2.
Similarly, using equation 1, angular momentum of the mass after the application of tension is given by
$L=mv'\left( \dfrac{{{R}_{0}}}{2} \right)$
where
$L$ is the angular momentum of mass
$m$ is the given mass
$v'$ is the velocity of mass, after the application of tension
$\dfrac{{{R}_{0}}}{2}$ is the radius of circular path, through which the mass rotates after the application of tension
Let this be equation 3.
Here, since we know that angular momentum is a conserved quantity, we can equate equation 2 and equation 3 as follows:
$L=m{{v}_{0}}{{R}_{0}}=mv'\left( \dfrac{{{R}_{0}}}{2} \right)\Rightarrow v'=2{{v}_{0}}$
Let this be equation 4.
Now, kinetic energy of the mass after the application of tension can be expressed as
\[KE=\dfrac{1}{2}m{{(v')}^{2}}=\dfrac{1}{2}m{{(2{{v}_{0}})}^{2}}=2m{{v}_{0}}^{2}\]
where
$KE$ is the kinetic energy of the mass after the application of tension
$m$ is the given mass
$v'$ is the velocity of mass, after the application of tension
${{v}_{0}}$ is the velocity of mass, before the application of tension
Let this be equation 5.
Therefore, from equation 5, it is clear that the final value of kinetic energy is equal to $2m{{v}_{0}}^{2}$ and hence, we can conclude that the correct answer is option $A$.
So, the correct answer is “Option A”.
Note: Tension on the mass refers to the pulling force exerted on the mass due to the string, which passes through the hole at the center, as given in the diagram above. Tension can be related to the action-reaction pair of forces acting on two ends of a string, cable or rod. Students can also try to understand the concept of tension from the famous tug-of-war game. Here, each team on either side of the rope suffers tension due to the other team.
Formula used:
$\begin{align}
& 1)L=mvr \\
& 2)KE=\dfrac{1}{2}m{{v}^{2}} \\
\end{align}$
Complete step-by-step answer:
When a particle rotates about an axis, angular momentum of the particle is defined as the product of mass of particle, velocity of particle and the radius of the circular path, through which the particle rotates. It is a conserved quantity. Mathematically, angular momentum is given by
$L=mvr$
where
$L$ is the angular momentum of a rotating particle
$m$ is the mass of particle
$v$ is the velocity of particle
$r$ is the radius of circular path, through which the particle rotates
Let this be equation 1.
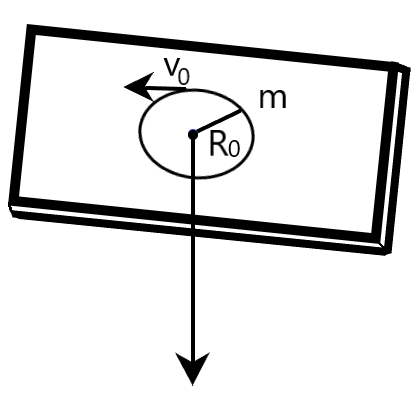
Coming to our question, we are given with a mass $m$, which moves in a circle on a smooth horizontal plane with velocity ${{v}_{0}}$, at a radius ${{R}_{0}}$. The mass is attached to a string which passes through a smooth hole in the plane as shown in the following figure. The tension in the string is increased gradually and finally, the mass $m$ moves in a circle of radius $\dfrac{{{R}_{0}}}{2}$. We are required to determine the final value of kinetic energy.

Let us assume the velocity of mass $m$, which when rotates in a circular path of radius $\dfrac{{{R}_{0}}}{2}$, to be $v'$.
Using equation 1, angular momentum of the mass before the application of tension is given by
$L=m{{v}_{0}}{{R}_{0}}$
where
$L$ is the angular momentum of mass
$m$ is the given mass
${{v}_{0}}$ is the velocity of mass, before the application of tension
${{R}_{0}}$ is the radius of circular path, through which the mass rotates before the application of tension
Let this be equation 2.
Similarly, using equation 1, angular momentum of the mass after the application of tension is given by
$L=mv'\left( \dfrac{{{R}_{0}}}{2} \right)$
where
$L$ is the angular momentum of mass
$m$ is the given mass
$v'$ is the velocity of mass, after the application of tension
$\dfrac{{{R}_{0}}}{2}$ is the radius of circular path, through which the mass rotates after the application of tension
Let this be equation 3.
Here, since we know that angular momentum is a conserved quantity, we can equate equation 2 and equation 3 as follows:
$L=m{{v}_{0}}{{R}_{0}}=mv'\left( \dfrac{{{R}_{0}}}{2} \right)\Rightarrow v'=2{{v}_{0}}$
Let this be equation 4.
Now, kinetic energy of the mass after the application of tension can be expressed as
\[KE=\dfrac{1}{2}m{{(v')}^{2}}=\dfrac{1}{2}m{{(2{{v}_{0}})}^{2}}=2m{{v}_{0}}^{2}\]
where
$KE$ is the kinetic energy of the mass after the application of tension
$m$ is the given mass
$v'$ is the velocity of mass, after the application of tension
${{v}_{0}}$ is the velocity of mass, before the application of tension
Let this be equation 5.
Therefore, from equation 5, it is clear that the final value of kinetic energy is equal to $2m{{v}_{0}}^{2}$ and hence, we can conclude that the correct answer is option $A$.
So, the correct answer is “Option A”.
Note: Tension on the mass refers to the pulling force exerted on the mass due to the string, which passes through the hole at the center, as given in the diagram above. Tension can be related to the action-reaction pair of forces acting on two ends of a string, cable or rod. Students can also try to understand the concept of tension from the famous tug-of-war game. Here, each team on either side of the rope suffers tension due to the other team.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




