Question

A mass $M{\text{ kg}}$ is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of $45^\circ $ with the initial vertical direction will be
A. $Mg\left( {\sqrt 2 + 1} \right)$
B. $Mg\sqrt 2 $
C. $\dfrac{{Mg}}{{\sqrt 2 }}$
D. $Mg\left( {\sqrt 2 - 1} \right)$

Answer 1

Hint: We are given a mass suspended by a weightless string and we need to find the horizontal force required to take the string to a point where it makes a required angle with the vertical. We need to balance the forces acting on the mass in opposite directions to keep the mass stable at the required position.

Complete step by step answer:
We know that when two bodies are in contact with each other, some forces known as contact forces act on the bodies. If one of the bodies is a mass suspended from a spring, a force called tension acts on the string.We will draw the diagram for the given situation to get a better understanding.

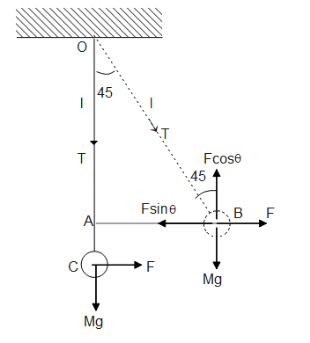
Now as we displace the mass the total work done will be equal to the change in kinetic energy.Therefore using the work-energy theorem we have
$W = \Delta K$
$\Rightarrow {W_T} + {W_{Mg}} + {W_F} = \Delta K$
Where ${W_T}$ is the work done by tension force, ${W_{Mg}}$ is work done by the weight of the mass and ${W_F}$ work done by the horizontal force applied.

Now work done by the tension force of the string will be zero as the tension of the string remains the same even after displacement. The work done by the weight of the mass will be equal to the product of the weight force and the displacement of the mass in the vertical direction. And work done by the force applied will be equal to the product of the horizontal force and horizontal displacement. Substituting the expressions for the three work done we get,
$0 + Mg \times AC + F \times AB = \Delta K$

The initial and the final velocity of the mass will be zero as it is taken from the rest position to another position at rest, therefore the change in kinetic energy of the mass will be zero.Hence,
$F = Mg\dfrac{{AC}}{{AB}}$
Now we can calculate the values of the distances using trigonometric ratios and Pythagoras theorem in the right-angle triangle formed in the figure.
$AC = OC - OA = l - l\cos 45^\circ = l(1 - \dfrac{1}{{\sqrt 2 }})$
And $AB = l\sin 45^\circ = l\dfrac{1}{{\sqrt 2 }}$
$F = Mg\left( {\dfrac{{1 - \dfrac{1}{{\sqrt 2 }}}}{{\dfrac{1}{{\sqrt 2 }}}}} \right)$
$\therefore F = Mg(\sqrt 2 - 1)$

Hence option D is the correct answer.

Note: Note that for calculating the work done by the weight of the mass, we considered the vertical displacement because the weight force of the mass is acting vertically downwards and for horizontal force, we considered the horizontal displacement.