Question

A mass $m$ hangs with the help of a string wrapped around a pulley on a frictionless bearing.
The pulley has a mass $m$ and radius $R$. Assuming pulley to be perfect uniform circular disc, the acceleration of the mass $m$, if the string does not slip on the pulley, is:
(A) $\dfrac{3}{2}g$
(B) $g$
(C) $\dfrac{2}{3}g$
(D) $\dfrac{g}{3}$

Answer 1

Hint: We can equate the two values of the torque on the pulley, from where we will get the tension. And we will also get the tension from the equation of the mass. Hence on equating the two tensions, we will get the acceleration of the mass.
In the solution we will be using the following formula,
$\Rightarrow \tau = TR$
where $\tau $ is the torque,
$T$ is the tension and $R$ is the radius of the pulley
$\Rightarrow \tau = I\alpha $
where $I$ is the moment of inertia and $\alpha $ is the angular acceleration.

Complete step by step solution:
We can draw the diagram of the pulley and the mass as,

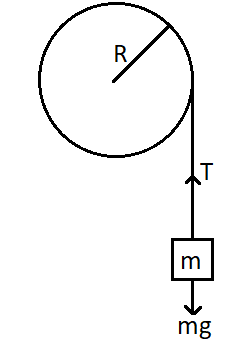
Due to the tension in the string and the mass of the pulley, there is a torque that is acting on the pulley. This torque is given by the formula,
$\Rightarrow \tau = TR$
Again, the torque can also be written as,
$\Rightarrow \tau = I\alpha $
Now the moment of inertia of the pulley is $I = \dfrac{{m{R^2}}}{2}$
and the angular acceleration can written in the terms of the linear acceleration as,
$\Rightarrow \alpha = \dfrac{a}{R}$
Now substituting these values we get the torque as,
$\Rightarrow \tau = \dfrac{{m{R^2}}}{2} \times \dfrac{a}{R}$
This value of torque can be equated with $\tau = TR$. So we get,
$\Rightarrow TR = \dfrac{{m{R^2}}}{2} \times \dfrac{a}{R}$
Cancelling all the common terms we get,
$\Rightarrow T = \dfrac{{ma}}{2}$
Now for the block of mass $m$, there is the tension acting on it upwards and the weight acting downwards. The resulting acceleration is in the downward direction. So we can write the equation of the mass as,
$\Rightarrow mg - T = ma$
Here we can substitute the value of the tension and take it to the RHS. So we get,
$\Rightarrow mg = ma + \dfrac{{ma}}{2}$
On cancelling all the $m$ and adding the RHS we get,
$\Rightarrow g = \dfrac{3}{2}a$
Therefore, we get the acceleration as,
$\Rightarrow a = \dfrac{2}{3}g$
So the correct answer is option (C).

Note:
In this problem we have found the equation for the mass that is attached to the pulley by considering the free body diagram of the said mass. The free body diagram is a simple figure of any body which shows the forces that are acting on the body with the help of arrows.