Question

A mass is being whirled in the horizontal circle with radius 1m and angular velocity $\omega = (t^2+t) rad/s$. Net acceleration acting on the mass, at t=1s from start is:
$\text{A.}\quad 5\ ms^{-2}$
$\text{B.}\quad 6\ ms^{-2}$
$\text{C.}\quad 3\ ms^{-2}$
$\text{D.}\quad 4\ ms^{-2}$

Answer 1

Hint: Motion in a circular path means that the velocity of the particle undergoing circular motion will always change its direction (along the tangent) with time. One should always take care of the difference between scalar and vector quantity. Speed is a scalar quantity and velocity is a vector quantity. If the speed is constant, it doesn’t imply that the acceleration is zero but if the velocity is constant, it always implies that acceleration is zero or motion is non-accelerated.
Formula used:
$a_c=\omega^2 R$

Complete answer:

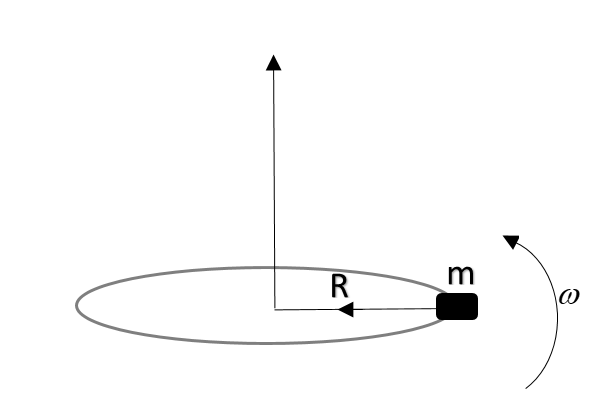
Here, we are asked to find the net acceleration of the particle at time ‘t=1 sec’. As a particle is undergoing circular motion, hence its acceleration will be centripetal acceleration given by $a_c=\omega^2 R$, where $\omega$ is the angular velocity at a particular instant and ‘R’ is the radius in which the particle is rotating.
Thus $a_c=\omega^2 R$
Now, $\omega = t^2+t$
At t=1 sec, $\omega = 1^2+1 = 2 rad/s$
Thus, $a_c=(2)^2 \times 1 = 4 m/s^2$
Thus option d. is correct.
Additional information: Vector form of centripetal acceleration is: $\vec a = -\omega^2 R ( sin \omega t\ \hat i + cos \omega t\ \hat j)$ which shows that its direction is towards the centre and along the string at every point of circular track.
$\vec a = -\omega^2 R ( sin \omega t\ \hat i + cos \omega t\ \hat j)$
To find the magnitude:
$|\vec a| = \omega^2 R \sqrt{(sin \omega t)^2 + (cos \omega t)^2}$=$\omega^2R$ [ $sin^2 \theta + cos^2 \theta = 1$]
Hence centripetal acceleration is $\omega^2 R$.

Note:
Students are strongly advised to keep a note on different physical quantities appearing before them, like speed is scalar and velocity is a vector quantity and if even the direction of velocity changes, it results in acceleration. One should always remember that whenever a body moves in a curve (basically changes its direction of motion), it will always experience centripetal force acting on it. In short, direction can’t be changed without the application of force. In the above case, the string is providing necessary centripetal force.