Question

A man wishes to swim across a river 0.5 km wide. If he can swim at the rate of 2 km/h in still water and the river flows at the rate of 1 km/h. The angle (w.r.t the flow of the river) along which he should swim so as to reach a point exactly opposite his starting point, will be:
(A) \[60^\circ \]
(B) \[120^\circ \]
(C) \[145^\circ \]
(D) \[90^\circ \]

Answer 1

Hint:The given problem can be seen as a problem based on the motion of a particle in a plane or relative motion in 2-Dimension. Relative motion can be defined as the motion of one particle with respect to another in a frame.

Step-by-step solution:
Step 1: Relative motion is a motion when motion of one particle in a given frame (say S) is seen from another frame (say S’) then the motion of particle is said to be relative w.r.t. frame S’.
In a relative motion position, velocity, and acceleration of a particle are measured in two different frames which are in relative motion w.r.t. each other.
For this problem, it is given that the rate at which river flows is 1 km/h (this can be seen as the relative velocity of river with respect to the ground i.e., \[\overrightarrow {\mathop V\nolimits_{R,G} } \]) and the rate at which man swims is 2 km/h (this can be seen as the relative velocity of man with respect to the river i.e., \[\overrightarrow {\mathop V\nolimits_{M,R} } \] ).
We can resolve this problem in a way that the relative motion of the river with respect to the ground is one frame and the relative motion of man with respect to the river is another frame.
Step 2: The given two velocities can be drawn in the shown figure below –

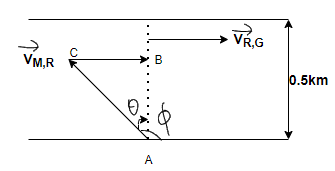
In the given circuit \[\overrightarrow {\mathop V\nolimits_{M,R} } = 2\]km/hr and \[\overrightarrow {\mathop V\nolimits_{R,G} } = 1\]km/hr, \[\theta \] is angle made by man w.r.t. normal, and \[\phi \] is an angle made by man w.r.t. river. So, we have to find \[\phi \] and that can be calculated as –
\[\phi = 90^\circ + \theta \] ………………………...…………….. (1)
Step 3: From the above figure we know the values of AC and BC so we can find the angle \[\theta \] by using the trigonometric identity –
\[\sin \theta = \dfrac{{BC}}{{AC}}\]; substituting the values of AC and BC
\[\sin \theta = \dfrac{1}{2}\]; rearranging the equation
\[\theta = \mathop {\sin }\nolimits^{ - 1} \left( {\dfrac{1}{2}} \right)\]
\[\theta = 30^\circ \]
Now, substituting the value of \[\theta \] in equation (1), we will get
\[\phi = 90^\circ + 30^\circ = 120^\circ \]
So, the angle made by the man w.r.t. The flow of the river is \[120^\circ \].

So, the correct option is (B).

Note: It should be remembered while solving these types of problems we have to assume that the meaning of time is the same in both the frames because the velocities are comparable. But if the velocities are not comparable then this assumption is wrong (for example if velocity of one body is comparable to speed of light and velocity of other body is very less).