Question

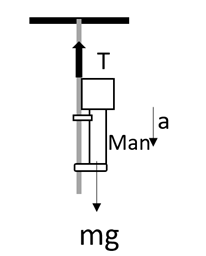
A man who is sliding down a light rope whose breaking strength will be $\eta $ times the weight of man $\left( \eta \langle 1 \right)$. What will be the maximum acceleration of the man so that the rope will just break?
$\begin{align}
  & A.g\left( 1-\eta \right) \\
 & B.g\left( \dfrac{1}{\eta } \right) \\
 & C.g\eta \\
 & D.\dfrac{g}{\eta } \\
\end{align}$

Answer 1

Hint: The maximum tension in the string will be equivalent to the product of the mass of the man and the acceleration due to gravity times $\eta $. The difference between the weight of the man and the maximum tension in the string will be equivalent to the product of the mass of man and the acceleration of the man. Using these equations, find out the acceleration of the man. This will help you in answering this question.

Complete answer: The maximum tension in the string will be equivalent to the product of the mass of the man and the acceleration due to gravity times $\eta $. This can be written as an equation given as,
${{T}_{\max }}=\eta mg$
The difference between the weight of the man and the maximum tension in the string will be equivalent to the product of the mass of man and the acceleration of the man. This can be written as,
$\begin{align}
  & mg-{{T}_{\max }}=ma \\
 & \Rightarrow mg-\eta mg=ma \\
\end{align}$
Cancelling the common terms in the equation can be shown as,
$a=g\left( 1-\eta \right)$
Hence the correct answer for the question has been calculated.

The acceleration of the man has been obtained as option A.

Note:
The tension in the string can be described as the pulling force which is axially transmitted by the means of a chain, a string, a cable, chain or in the each end of the rod. The primary difference between the tension and the force will be the direction of force. Tension will be the force which is pulling something apart. This will be always acting in the direction of the string.