Question

A man who can swim at a velocity v relative to water wants to cross a river of width b flowing with a speed u.
This question has multiple correct options.
A. the minimum time in which he can cross the river is $\dfrac{b}{v}$
B. he can reach a point exactly opposite on the bank in time $t=\dfrac{b}{\sqrt{{{v}^{2}}-{{u}^{2}}}}$ if $v>u$
C. he cannot reach the point exactly opposite on the bank if $u>v$
D. he cannot reach the point exactly opposite on the bank if $v>u$

Answer 1

Hint: We are given the relative velocity of the man with respect to the flow of water. Obtain the component of velocity of the man along the flow of water and in its perpendicular direction. Find the minimum time required using the velocity perpendicular to the flow of water.

Complete step by step solution:

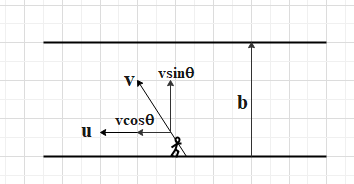
A man is swimming in a river with velocity v relative to the river. Where the water flows with a speed u.
Let, the velocity v makes an angle of $\theta $ with the velocity of the river u.
So, the component of velocity of the swimming man in the direction of flow of water will be $v\cos \theta $ and in the perpendicular direction of flow of water will be $v\sin \theta $ .
Now, to cross the river in minimum time the component of velocity $v\sin \theta $ should be maximum.
For $v\sin \theta $ to be maximum, the $\sin \theta $ should be maximum and for this $\theta =\pi /2$
At $\theta =\pi /2$, $v\sin \theta $ will be v.
The width of the river is b.
So, the minimum time taken to cross the river will be,
${{t}_{\text{min}}}=\dfrac{b}{v}$
Again, to reach a point exactly opposite on the bank, net velocity of the man will be,
$\sqrt{{{v}^{2}}-{{u}^{2}}}$ where, $v>u$
He cannot reach the exact opposite point if $u>v$
Hence, the time taken by the man to reach the point exactly opposite on the bank is,
$t=\dfrac{b}{\sqrt{{{v}^{2}}-{{u}^{2}}}}$
So, correct options are (A), (B) and (C)

Note: We can directly say that to cross the river to the point directly opposite to the bank, the velocity of swimming of the man should always be larger than the velocity of flow of water of the river. If the velocity of the flow of the river is larger than the velocity of the man, he can never reach the point directly opposite to the bank.