Question

A man walks 4 km due north in one hour and 3 km in the next hour. What is his average velocity?
A. $2.5km/h,{37^ \circ }EofN$
B. $3.5km/h,{37^ \circ }EofS$
C. $5km/h,{37^ \circ }EofN$
D. $2.5km/h,{37^ \circ }EofE$

Answer 1

Hint: average velocity is the ratio of displacement i.e., shortest distance and time taken by the man. Displacement is obtained from the Pythagoras theorem as it forms a right angle triangle.

Complete step by step answer:A man walks 4 km in the direction of the north in one hour and now he walks 3 km in the north direction (this direction is taken from where he is standing) in another one hour.

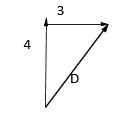
The displacement D is the shortest route between the initial and final position of the man. The above triangle forms a right angle triangle. Hence, it will obey the Pythagoras theorem which states that
${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {base} \right)^2} + {\left( {height} \right)^2}$
$\Rightarrow {D^2} = {4^2} + {3^2}$
$\Rightarrow {D^2} = 16 + 9$
$\Rightarrow D = \sqrt {25} $
$\Rightarrow D = 5km$
The average velocity of the man is defined as the total displacement divided by the total time taken by him.
Total time taken =$1 + 1 = 2hours$
Average velocity = $\dfrac{{total{\text{ }}displacement}}{{total{\text{ }}time{\text{ }}taken}}$
$\Rightarrow $Average velocity = $\dfrac{5}{2} = 2.5km/h$
The angle $Ɵ$ is given by tangent of the angle between displacement and initial position
$\tan \theta = \dfrac{{height}}{{base}}$
$\Rightarrow \tan \theta = \dfrac{3}{4}$
 $\Rightarrow \theta = \arctan \left( {\dfrac{3}{4}} \right)$
$\Rightarrow \theta = {36.86^ \circ } = {37^ \circ }\left( {approx.value} \right)$
The final position is ${37^ \circ }$ east of north as compared to the initial position.
Therefore, option A is correct.

Note:In the given figure, upward direction represents north side, downward I.e., bottom of north represents south, left side represents west and right side is east.