Question

A man swims across a river with speed of $5km{h^{ - 1}}$(in still water), while a boat goes upstream with speed $12km{h^{ - 1}}$(in still water). How fast and in which direction does the man appear to go to the boatman? Given that the speed of flowing water is$2km{h^{ - 1}}$_.

Answer 1

Hint: The vector resultant can be used to solve this problem. The direction of the boat is perpendicular to the velocity of the stream and therefore the resultant velocity of the boat will be in the resultant of the velocities of the stream and the boat.

Complete Step by step solution:
It is given in the problem that a man swims across a river with speed of $5km{h^{ - 1}}$(in still water), while a boat goes upstream with speed $12km{h^{ - 1}}$(in still water) and we need to tell in which direction and with what speed the man appears from the boat, if the speed of flowing water is$2km{h^{ - 1}}$_.

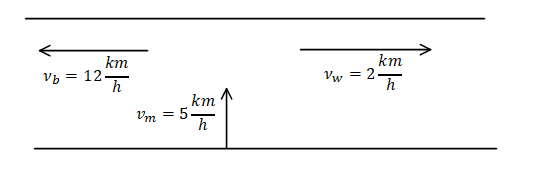
The velocity of the boat with respect to the river is given by,
$ \Rightarrow {v_{b,m}} = \sqrt {{2^2} + {{12}^2}} $
$ \Rightarrow {v_{b,m}} = \sqrt {4 + 144} $
$ \Rightarrow {v_{b,m}} = \sqrt {4 + 144} $
$ \Rightarrow {v_{b,m}} = \sqrt {148} \dfrac{m}{s}$………eq. (1)
The relative velocity of the man with respect to river is given by,
$ \Rightarrow {v_{m,r}} = \sqrt {{2^2} + {5^2}} $
$ \Rightarrow {v_{m,r}} = \sqrt {4 + 25} $
$ \Rightarrow {v_{m,r}} = \sqrt {29} \dfrac{{km}}{h}$……….eq. (2)
The direction in which the man appear to move from the boatman is given by,
$ \Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{{{v_{m,r}}}}{{{v_{b,m}}}}} \right)$
Replacing the values of ${v_b}$ and ${v_m}$ in the above relation from equation (1) and equation (2) we get.
$ \Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{{{v_{m,r}}}}{{{v_{b,m}}}}} \right)$
$ \Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{{\sqrt {29} }}{{\sqrt {148} }}} \right)$
$ \Rightarrow \theta = {\cos ^{ - 1}}\left( {\sqrt {\dfrac{{29}}{{148}}} } \right)$.
$ \Rightarrow \theta = 63 \cdot 72^\circ $
The speed with which the man appears by the boat is given by,
$ \Rightarrow v = \sqrt {148 - 29} $
$ \Rightarrow v = \sqrt {119} \dfrac{{km}}{h}$.
The velocity of the man that appears from the boat is equal to $V = \sqrt {119} \dfrac{m}{s}$ and the direction in which the man appears is equal to$\theta = 63 \cdot 72^\circ $.

Note: The concept of resultant vector is very important and students need to understand and remember this concept. Whenever we cross a river then we cross it the way in which we can cross it in minimum time.