Question

A man standing on a railway platform noticed that a train took 21 seconds to cross the platform (this means the time elapsed from the moment the engine enters the platform till the last compartment leaves the platform) which is 88 meters long and that it took 9 seconds to pass him. Assuming that the train was moving with uniform speed. What is the length of the train in meters?
(A) 55
(B) 60
(C) 66
(D) 72

Answer 1

Hint: Assume that the length of the train is x meters and the speed of the train is v m/s. Here, we have two cases. In the first case, it is given that the train takes 21 seconds to cross the platform which is 88 meters long. The train covers the distance equal to the summation of the length of the train and the length of the platform to cross the platform. Now, use the formula, \[\text{Time=}\dfrac{\text{Distance}}{\text{Speed}}\] and get an equation in terms of x and v. In the second case, it is given that the train takes 9 seconds to cross a man standing on the platform. The train covers the distance equal to the length of the train to cross a man standing on the platform. Now, use the formula, \[\text{Time=}\dfrac{\text{Distance}}{\text{Speed}}\] and get an equation in terms of x and v. Now, we have two equations in terms of x and v, and then, solve it further to get the value of x.

Complete step-by-step solution:
First of all, let us assume that the length of the train is x meters and the speed of the train is v m/s.
The length of the train = x meters ………………………………………..(1)
The speed of the train = v m/s …………………………………………..(2)
Here, we have two cases.
In the first case, we have been given that the train takes 21 seconds to cross the platform which is 88 meters.
The time is taken to coss the platform = 21 seconds …………………………………..(3)
The length of the platform = 88 meters …………………………………………..(4)
From equation (1) and equation (4), we have the length of the train and the length of the platform.
From the figure, we can see that the train covers the distance equal to the summation of the length of the train and the length of the platform to cross the platform.

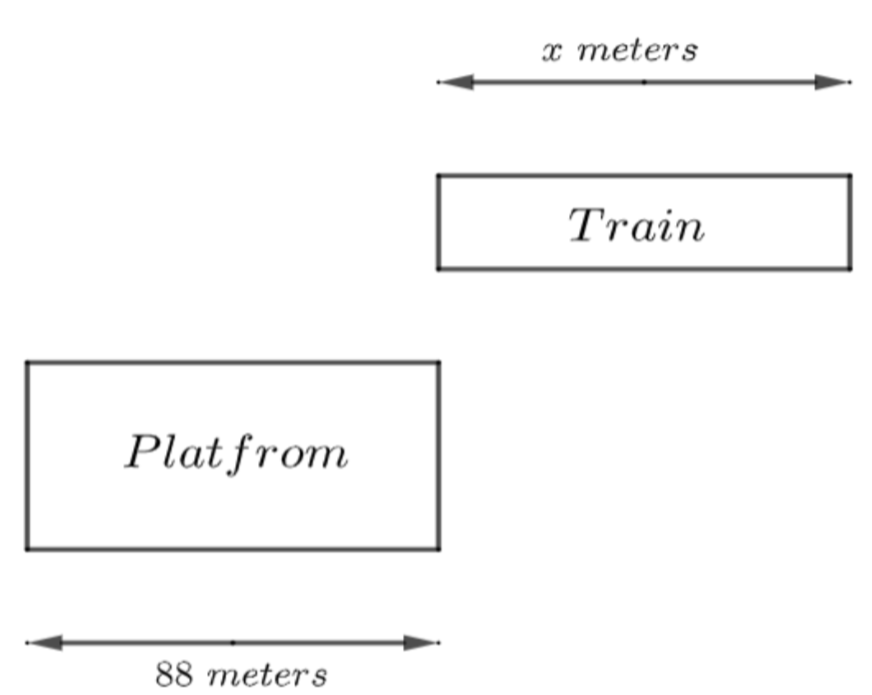
The distance to be covered by the train to cross the platform = \[\left( x+88 \right)\] meters …………………………………….(5)
We know the formula, \[\text{Time=}\dfrac{\text{Distance}}{\text{Speed}}\] …………………………………………(6)
Now, from equation (2), equation (3), and equation (6), we get
\[\Rightarrow 21\text{=}\dfrac{\left( x+88 \right)}{v}\] …………………………..(7)
In the second case, we have been given that the train takes 9 seconds to cross a man standing on the platform.
The time is taken to cross a man standing on the platform = 9 seconds …………………………………..(8)

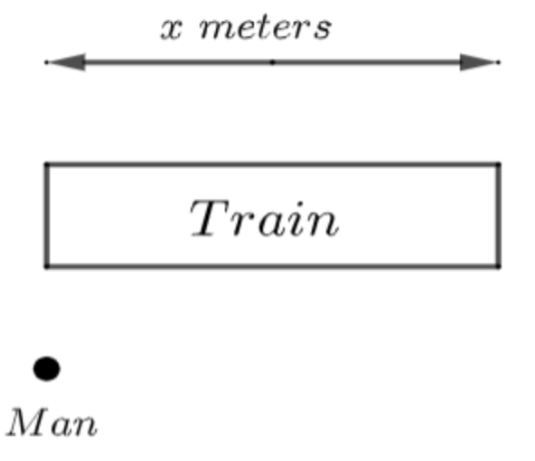
From the figure, we can see that the train covers the distance equal to the length of the train to cross a man standing on the platform.
From equation (1), we have the length of the train.
The length of the train = x meters.
Now, from equation (1), equation (2), and equation (8), we get
\[\Rightarrow 9\text{=}\dfrac{x}{v}\]
\[\Rightarrow v=\dfrac{x}{9}\] …………………………..(9)
Now, substituting the value of v from equation (9) in equation (7), we get
\[\begin{align}
  & \Rightarrow 21\text{=}\dfrac{\left( x+88 \right)}{\dfrac{x}{9}} \\
 & \Rightarrow 21\times \dfrac{x}{9}=\left( x+88 \right) \\
 & \Rightarrow \dfrac{7x}{3}-x=88 \\
 & \Rightarrow \dfrac{7x-3x}{3}=88 \\
 & \Rightarrow \dfrac{4x}{3}=88 \\
 & \Rightarrow x=\dfrac{88\times 3}{4} \\
 & \Rightarrow x=22\times 3 \\
\end{align}\]
\[\Rightarrow x=66\] …………………………………….(10)
Now, from equation (1) and equation (10), we get
The length of the train = 66 meters.
Hence, the correct option is (C).

Note: In this question, one might take the distance covered by the train to cross the platform equal to 88 meters. This is wrong because the length of the train is x meters and to cross the platform, the last compartment of the train must also cross the platform. Therefore, the distance covered by the train to cross the platform should be equal to \[\left( x+88 \right)\] meters.